Hallar la ecuacion de la circunferencia

;)
Hola Gustavo!
Buscamos la intersección de las dos circunferencias:

$$\begin{align}&x^2+y^2-6x+4=0\\&x^2+y^2-2=0\\&\\&restándolas:\\&-6x+6=0\\&x=1\\&sustituyendo \ en \ la \ segunda:\\&1+y^2-2=0\\&y^2=1\\&y=\pm1\\&\\&puntos \ intersección:\\&(1,1)\\&(1,-1)\\&el \ centro \ de \ la \ circunferencia \ buscada \ equidista \ de \ esos \dos \ puntos,\ luego\\&está \ en \ su \ mediatriz que \es \ el\ eje \ x.Luego centro \ es\\&D=(d,0)\\&radio=distancia(D,t)\\&t:recta \ tangente:x+3y-14=0\\&\\&r=\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}=\frac{|d-14|}{\sqrt{3^2+1^2}}=\frac{|d-14|}{\sqrt{10}}\\&\\&ecuación \ circunferencia \ buscada:\\&(x-d)^2+y^2=\Big(\frac{|d-14|}{\sqrt{10}} \Big)^2\\&(x-d)^2+y^2=\frac{d^2-28d+196}{10}\\&\\&el \ punto \ (1,1) \ pasa \ por \ esa\ circunferencia:\\&\\&(1-d)^2+1=\frac{d^2-28d+196}{10}\\&\\&\\&(1-2d+d^2+1)10=d^2-28d+196\\&\\&9d^2+8d-176=0\\&\Rightarrow\\&d_1=4 \Rightarrow r_1=\frac{|4-14|}{\sqrt {10}}=\frac{10}{\sqrt{10}}=\sqrt {10} \Rightarrow(x-4)^2+y^2=10\\&\\&solución2:\\&d_2=\frac{-44}{9} \Rightarrow r_2=\frac{|-\frac{44}{9}-14|}{\sqrt{10}}=\frac{170}{9 \sqrt{10}} \Rightarrow \\&\\&(x+\frac{44}{9})^2+y^2=(\frac{170}{9 \sqrt{10}})^2=\frac{2890}{81}\end{align}$$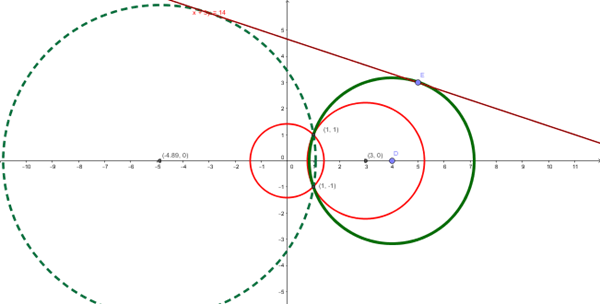

Saludos

;)

;)