Anónimo
Como resolver ejercicio de probabilidad numero 9
·
·
¡Hola Anónimo!
Cuando Lucas te conteste haz el favor de subirle la nota a Excelente. Repondemos bien las preguntas y no te cuesta nada votar de esa forma.
Lo que no entiendo es porque te dicen que no apliques la corrección por continuidad, es algo que siempre se hace pero no lo haré ya que lo dicen.
Dada una distribución binomial con las condiciones de más de 30 lanzamientos y con np >= 5 y n(1.p)>= 5 se puede usar la aproximación por una distribución normal con estos parámetros.
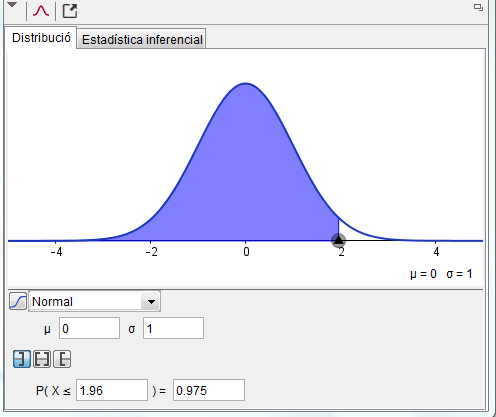
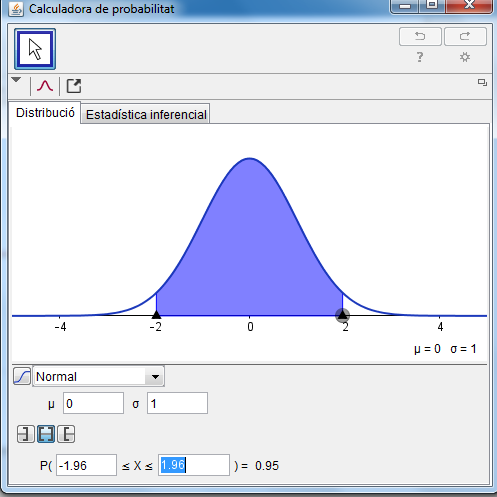
$$\begin{align}&\mu= np = 100·0.9 = 90\\&\\&\sigma = \sqrt{np(1-p)}= \sqrt{100·0.9·0.1}=3\\&\\&\text{Es una }N(90,3)\\&\\&\text{Podríamos tomar infinitos intervalos (a,b)}\\&\text{pero se supone que es el centrado en la media}\\&\\&\text{Entonces debemos calcular el valor que deja}\\&\text{a la izquierda una probabilidad de 0.975}\\&\\&\text{Es un valor superconocido z=1.96}\\&\\&\text{Luego la binomial tipificada debe valer 1.96}\\&\\&Z=\frac{X-90}{3}=1.96\\&\\&X-90= 5.88\\&\\&\text{Ese el radio del intervalo, luego la longitud es el doble}\\&\\&L= 2·5.88 = 11.76\end{align}$$Y eso es todo, saludos.
:
:
¡Gracias! Respecto lo de la votación, le he dado sin querer porque mi ratón no funciona bien, y no se porqué pero no me deja cambiarlo, ya no pasará más! :)
1 respuesta más de otro experto
;)
Hola Anónimo!
Se entiende que es un intervalo centrado en la media.
Luego queda una cola superior e inferior de probabilidad
$$\begin{align}&\frac{1-0.95}{2}=0.025\end{align}$$luego en la tabla de la normal tipificada hemos de encontrar el valor de z que corresponde a una probabilidad de 1-0.025=0.9750
que corresponde a z=1.96
luego el intervalo centrado es:
buscando el valor de x
$$\begin{align}&z=\frac{x- \mu}{\sigma}\\&\\&x=\mu+z \sigma\\&\\&\mu=np=100·0.9=90\\&\\&\sigma=\sqrt{npq}=\sqrt{100·0.9·0.1}=3\\&\\&x_1=90+1.96·3=95.88=b\\&x_2=90-1.96·3=84.12=a\\&\\&longitud=b-a)=11.76\end{align}$$saludos
;)
;)