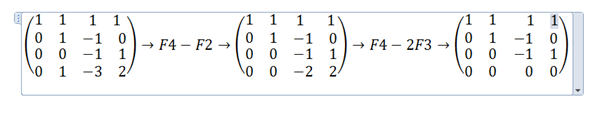Cómo se resuelve este problema de subespacios?
Encuentra una base para el subespacio de P3 (polinomios de grado menos o igual que 3) generado por los polinomios : p(x) 1-x, q(x) = -x+x², r(x)= 1+x+x²+x³, s(x)= 2-3x+x²
1 respuesta
Respuesta de Lucas m
1
;)
Hola Miguel!
Escribimos los vectores asociados:
Son polinomios de grado 3, escribo los coeficientes de cada término de grado mayor a menor:
p(x)=(0,0,-1,-1)=-x-1
q(x)=(0,1,-1,0)=x^2-x
r(x)=(1,1,1,1)=x^3+x^2+x+1
s(x)=(0,1,-3,2)
escribo la matriz y la triangulo:
dimE=3
Base: los tres vectores no nulos de la matriz triangulada:
B
$$\begin{align}&B=\{x^3+x^2+x+1,x^2-x,x^2-x+1 \}\end{align}$$saludos
;)
;)
