ayúdenme con este ejercicio
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Alex Mate!
No sé por qué han sido tan malvados de poner funciones de y, no entiendo lo que pretenden que hagamos. El área va a ser la misma llamando x a la dependiente y y a la independiente que si lo hacemos al revés. Así que voy a ignorar por completo esa cuestión y haré la gráfica como si fueran funciones de x.
h(x) = x^2 - 1
g(x) = x^2 - (1/8)x^4 + 1
Esta es la gráfica.
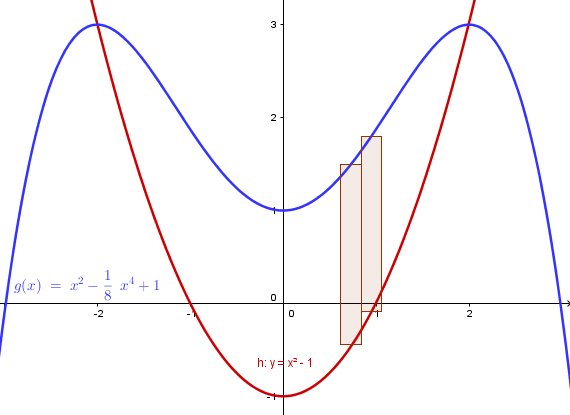
Tienes dibujudos dos de esos diferenciales de área.
Debemos ver los puntos de corte de las dos curvas, por el dibujo parece que son (-2,3) y (2,3) veriquémoslo
g(-2) = 4 - 2 + 1 = 3
h(-2) = 4-1 = 3
g(-2) = 4-2+1=3
g(2) = 4-1 = 3
Además vemos que las figuras son simétricas respecto del eje Y, eso simplifica un poco las cuentas
$$\begin{align}&A=2\int_0^2\left(x^2-\frac 18x^4+1 -(x^2-1) \right)dx=\\&\\&2\int_0^2\left(-\frac 18x^4+2 \right)dx=\\&\\&2\left[-\frac{x^5}{40}+2x \right]_0^2=2\left(-\frac{32}{40}+4 \right)=\\&\\&2\left(-\frac 45+4 \right)=2·\frac {16}5=\frac {32}5\end{align}$$Y eso es todo, sa lu dos.
:
:
