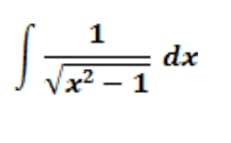El tema es de análisis matemáticas calculo
Elige los temas de la pregunta Elige los temas de la pregunta Elige los temas de la pregunta
2 Respuestas
¡Gracias!
Resolver las siguientes integrales enunciando claramente la técnica o propiedad usada.
eso sola mente me dijeron
Pues si se conocen las funciones hiperbólicas y sus propiedades que puedes ver en el artículo de la wikipedia sobre funciones hiperbólicas es sencillo. Unicamente que yo voy a usar otras abreviaturas que son las que yo aprendí y son mejores
$$\begin{align}&sh\,x=\text{seno hiperbólico de x}\\&ch\,x=\text{coseno hiperbólico de x}\\&th\,x=\text{tangente hiperbólica de x}\\&\\&argsh\,x=\text{argumento del seno hiperbólico de x}\\&argch\,x=\text{argumento del coseno hiperbólico de x}\\&\\&\text{Las propiedades que interesan para esta integral son:}\\&ch^2x-sh^2x=1\\&\text{Con lo cual}\\&ch^2x-1=sh^2x\\&\text{que viene ni que pintado para deshacer la raíz}\\&\text{cuadrada del denominador de la integral}\\&\\&\text{Otras propiedades son:}\\&(ch\,x)'=sh\,x\\&(sh\,x)'=ch\,x\\&\\&\int \frac{1}{\sqrt {x^2-1}}dx=\\&\\&x=ch\,t\implies t = argch\,x\\&dx=sh\,t\;dt\\&\\&\int \frac{sh\,t}{\sqrt{ch^2t-1}}dt=\int \frac{sh\,t}{\sqrt{sh^2t}}dt=\\&\\&\int dt = t+C = argch\,x+C=\\&\\&\text{Y la traslación a funciones conocidas del }argch\,x\\&\text{la tienes en ese mismo artículo de la wikipedia}\\&\\&= ln(x+\sqrt{x^2-1})+C\end{align}$$No había puesto el articulo porque al poner la referencia te ponen medía página y es una molestia. Ahora que ya estamos al final lo pongo, pero seguramente no te saldrá entero luego tendrás que consultarlo de todas las formas.
https://es.wikipedia.org/wiki/Funci%C3%B3n_hiperb%C3%B3lica
·
Y eso es todo, sa lu dos.
:
:
¡Ah! Pues no ha sido tan grave como otras veces lo que han puesto que metían 100 líneas a lo mejor.
Y la otra alternativa para resolver la integral es un cambio trigonométrico, el artilugio para reventar la raíz cuadrada es que
1+tg^2(x) = sec^2(x)
sec^2(x) - 1 = tg^2(x)
$$\begin{align}&\int \frac{dx}{\sqrt{x^2-1}}=\\&\\&x=sec\,t \implies t=arcsec\,x\\&dx=sec\,t·tg\,t\;dt\\&\\&=\int \frac{sec\,t·tg\,t}{\sqrt{sec^2t-1}}dt=\int \frac{sec\,t·tg\,t}{\sqrt{tg^2t}}dt=\\&\\&\int sec\,t\;dt=\end{align}$$Y respecto a esta integral no es nada fácil. En algunos textos la ponen como inmediata pero no es fácil, no sale de una deducción rápida como las que sí que son integrales inmediatas
$$\begin{align}&\int \frac{dt}{cost}=\\&\\&tg \frac t2=u\\&\\&\text{las dos fórmulas de abajo se pueden}\\&\text{deducir pero las copio de un libro}\\&\\&cost=\frac{1-u^2}{1+u^2}\\&\\&dt = \frac {2du}{1+u^2}\\&\\&=\int \frac{1+u^2}{1-u^2}·\frac {2du}{1+u^2}=\int \frac{2du}{1-u^2}=\\&\\&\int \frac{2du}{(1+u)(1-u)}=\int \frac{du}{1+u}+\int \frac{du}{1-u} =\\&\\&ln|1+u| - ln|1-u| +C=\\&\\&ln\left|1+tg \frac t2\right|-ln\left|1-tg \frac t2\right|+C=\\&\\&ln\left|\frac{1+tg \frac t2}{1-tg \frac t2} \right|+C=ln \left|\frac{\left(1+tg \frac t2\right)^2}{1-tg^2 \frac t2}\right|+C=\\&\\&ln\left|\frac{\frac{(\cos \frac t2+sen \frac t2)^2}{\cos^2 \frac t2}}{\frac{\cos^2 \frac t2-sen^2 \frac t2}{\cos^2 \frac t2}} \right|+C=ln\left|\frac{1+2cos \frac t2sen \frac t2}{cost}\right|+C=\\&\\&ln\left|\frac{1+sent}{cost} \right|+C=ln\left|sec\,t+tg\,t \right|+C=\\&\\&ln|sec(arcsec\,x)+tg(arcsen\,x)|+C=\\&\\&ln\left|x+tg\left(arccos \frac 1x\right)\right|+C=\\&\\&ln \left|x+ tg\left(arctg \frac{\sqrt{1- \frac 1{x^2}}}{\frac 1x} \right) \right|+C=\\&\\&ln \left|x+ tg\left(arctg \frac{\frac 1x \sqrt{x^2- 1}}{\frac 1x} \right) \right|+C=\\&\\&ln \left|x+ tg\left(arctg \sqrt{x^2- 1}\right) \right|+C=\\&\\&ln \left|x+ \sqrt{x^2- 1} \right|+C\end{align}$$Y eso es todo, sa lu dos.
:
:
;)
Hola Andres!
Esa integral se puede hacer de varias maneras, pero la más sencilla es mediante una sustitución hiperbólica:
$$\begin{align}&x=cosht\\&dx=senht \ dt\\&\\&\int \frac{1}{\sqrt{x^2-1}}dx= \int \frac{1}{ \sqrt {cosh^2t -1}} senh t \ dt=\\&\\&\int \frac{senht}{\sqrt {senh^2t}}dt= \int dt=t=argcoshx+C=\\&\\&=ln(x+ \sqrt {x^2-1})+C\end{align}$$Saludos
;)
;)