Colaboración para resolver las siguientes integrales impropias
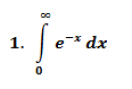
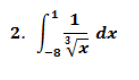
Ayudar para resolver las siguientes integrales impropias, de la materia de calculo
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
