Desarrollo de uno de los siguientes ejercicio de integrales
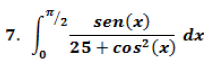
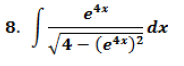
Requiero de ayuda para el desarrollo de algunos ejercicios propuestos por calculo.
2 respuestas
Respuesta de Lucas m
2
Respuesta de Valero Angel Serrano Mercadal
1
