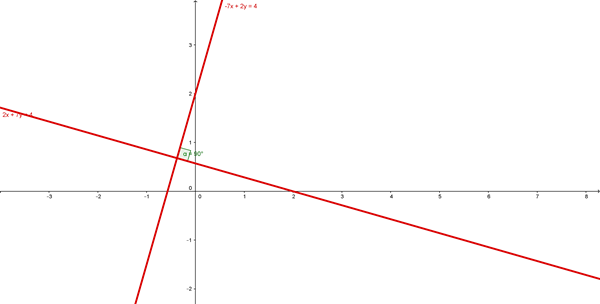
Dadas las ecuaciones de las lineas rectas
L1: 2x + 7y= 4 y L2: 2y-7x: 4
a. Graficas en un mismo plano cartesiano
b. Halle el valor de sus pendientes
c. Analiza lo que sucede al comparar el valor de las dos pendientes
d. ¿Cómo son las lineas L1 y L2?
Respuesta de Lucas m
1
;)
Hola angela pedroza!
b) Si escribes la ecuación explicita de la recta : y=mx+b
La pendiente es el coeficiente de la x.
Para ello despejamos la y en las dos ecuaciones:
$$\begin{align}&L_1\\&2x+7y=4\\&\\&7y=4-2x\\&\\&y=\frac{4}{7}- \frac{2}{7}x\\&\Rightarrow pendiente:\\&m=\frac{ -2}{7}\\&\\&L_2:\\&2y-7x=4\\&2y=7x+4\\&\\&y=\frac{7}{2}x+2\\&m=\frac{7}{2}\\&c)\\&Al \ multiplicarlas:\\&m_1·m_2=\frac{7}{2}· \frac{-2}{7}=-1\\&\\&d)\\&Perpendiculares\end{align}$$Este ejercicio estápuesto para que saque la conclusión:
El producto de las pendientes de dos rectas perpendiculares es -1
m·m'=-1
Saludos
;)
;)
