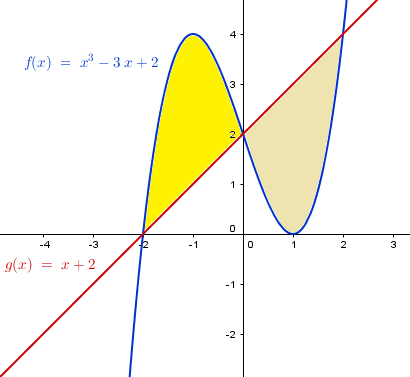
Quien me resuelve este problema de calculo

.... .... .... .... .... .... .... ... .... .... .... .... .... .... .... .... .... .... .... .... .... .... .... ...
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1