Anónimo
Como hallar el área en común entre los 2 círculos
Dos circunferencias con igual radio r son secantes. Hallar el área de la región común de los dos círculos, si se sabe que el centro de cada uno de ellos está sobre la circunferencia del otro
1 respuesta
Respuesta de Lucas m
2
;)
Hola !
La situación es la siguiente:
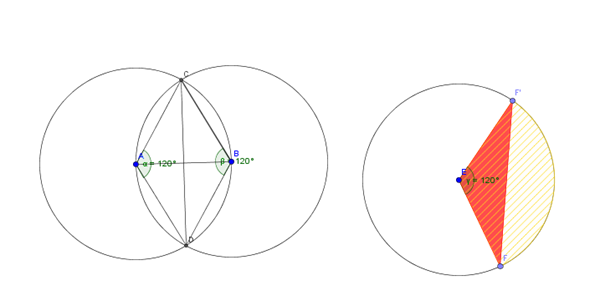
Los triángulos ABC y ABD son equiláteros pues todos los lados son iguales al radio r.
Por lo tanto el ángulo CAD=2·60º=120º
El área común es dos veces el área del Segmento Circular CBD=FF'
Area Segemento circular= Area Sector circular EFF' - Area triángulo EFF'=
$$\begin{align}&= \pi r^2 \frac{120º}{360º}- \frac{1}{2}r^2 sen120º=\\&\\&\pi r^2 \frac{1}{3}-\frac{1}{2} r^2 \frac{ \sqrt 3}{2}=\\&\\&r^2 \Big(\frac{\pi}{3}-\frac{ \sqrt 3}{4} \Big)\\&\\&Area_{comun}=2r^2 \Big(\frac{\pi}{3}-\frac{ \sqrt 3}{4} \Big)\end{align}$$Para calcular el área del triángulo he utilizado la Fórmula Trigonométrica:
$$\begin{align}&A=\frac{1}{2} a·b·sen \alpha\end{align}$$donde a y b, son dos lados contiguos y alfa el ángulo comprendido.
Esta fórmula es muy útil para calcula áreas de triángulos. En nuestro caso a=b=r
y alfa=120º
Saludos
;)
;)