Calcular limites tabular y graficar la función

·

·

¡Hola Diego!

Es una pregunta muy larga. Sobre todo la parte de las gráficas con Excel. Contestaré aquí solo a lo de los límites y la otra parte la mandas en otra pregunta.

$$\begin{align}&1) \quad \lim_{x\to 1}\frac{1}{x-1}= \frac 10=\pm\infty\\&\\&\\&2) \quad \lim_{x \to 1} \frac{\sqrt x-1}{x-1}= \frac{1-1}{1-1}= \frac{0}{0}\\&\\&\text{multiplicamos y dividimos por el conjugado del numerador}\\&\\&\lim_{x \to 1} \frac{\sqrt x-1}{x-1}·\frac{\sqrt x+1}{\sqrt x+1}=\\&\\&\lim_{x\to 1} \frac{(\sqrt x)^2-1^2}{(x-1)(\sqrt x + 1)}=\\&\\&\lim_{x\to 1} \frac{x-1}{(x-1)(\sqrt x + 1)}=\\&\\&\lim_{x\to 1} \frac{1}{\sqrt x + 1}= \frac{1}{\sqrt 1+1} = \frac 1{1+1}=\frac 12\\&\\&\\&\\&3)\quad \lim_{x\to 3} \frac{x^2+4x-21}{x^3-5x^2-2x+24}=\frac{9+12-21}{27-45-6+24}=\frac 00\\&\\&\text{Debemos sacar factor común (x-3)}\\&\text{en el numerador y denominador.}\\&\\&\text{En el numerador es sencillo}\\&x^2+4x-21=(x-3)(x+7)\\&\end{align}$$

En el denominador no lo es tanto, hay que hacer la división entera o la sintética (Ruffini) y eso se escribe muy mal aquí, usaremos Excel

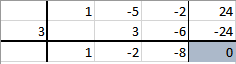
Luego el límite queda:

$$\begin{align}&=\lim_{x\to 3} \frac{(x-3)(x+7)}{(x-3)(x^2-2x-8)}=\\&\\&\lim_{x\to 3} \frac{x+7}{x^2-2x-8}=\frac{3+7}{9-6-8}=-\frac{10}{5}=-2\\&\\&\text{La respuesta que te ponen está mal}\\&\\&\\&\\&4)\lim_{x\to 1}log\, x^2 = log\,1^2=log \,1=0\\&\end{align}$$

Y eso es todo.  Recuerda mandar otra pregunta para las gráficas.

Sa lu dos.

:

: