Como hallar el área de 2 circunferencias?
Mi pregunta es la siguente.
Si tengo 2 circunferencias con igual radio r son secantes, como hallo el área de la legión común de los 2 círculos, si se sabe q el centro de cada uno de ellos está sobre la circunferencia del otro!
1 Respuesta
·
·
¡Hola SCORPEON!
Voy a hacer una gráfica para que sea más claro.
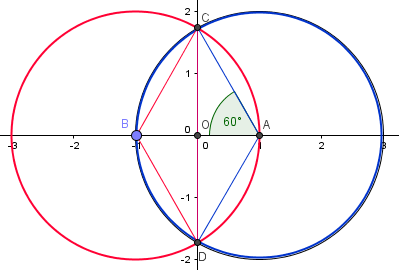
La región común de los dos círculos es la unión de dos segmentos circulares, el CAD y el CBD. Como las dos circunferencias son iguales calculamos el área de uno y la multiplicamos por dos. Para saber el área de un segmento circular debemos saber el ángulo correspondiente al sector.
En el dibujo vemos un ángulo de 60º que es la mitad del del sector ACD, luego el ángulo del sector es 120º.
¿Qué por qué ese ángulo que he puesto es 60º?
SI te fijas el segmento AO mide R/2 entonces el cateto adyacente entre la hipotenusa del triángulo ACO es el seno de ese angulo
sen(alfa)= (R/2) / R = 1/2
alfa = 60º
El área de un sector de 120º es
As = (120º/360º)Pi·r^2 = (1/3)Pi·r^2
Y para calcular el área del segmento CBD hay que restarle la del triángulo ACD
Este triangulo ACD tendrá base CD y altura OA por lo que su área es
$$\begin{align}&A_t = \frac{(2r·sen\,60º)·(r·\cos\,60º)} 2 = r^2·sen60º·cos60º = \\&\\&r^2·\frac{\sqrt 3}{2}·\frac 12= \frac{\sqrt 3}{4}r^2\\&\\&\text{Por lo tanto el areá de un segmento es}\\&\\&A_{sg}=\frac 13 \pi r^2-\frac{\sqrt 3}{4}r^2=\left(\frac 13 \pi-\frac{\sqrt 3}{4} \right)r^2\\&\\&\text{Como son dos segmentos, el área común es}\\&\\&A=\left(\frac 23 \pi-\frac{\sqrt 3}{2} \right)r^2\approx 1.228369699\,r^2\\&\end{align}$$:
:
