Tabular y graficar las siguiente funciones
Ayuda a la resolución del siguiente ejercicio.
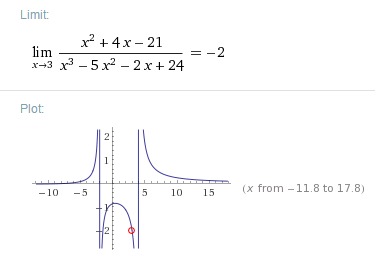
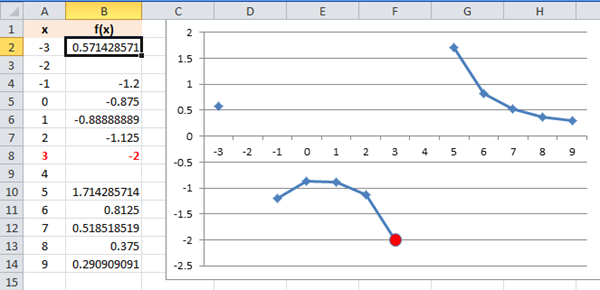
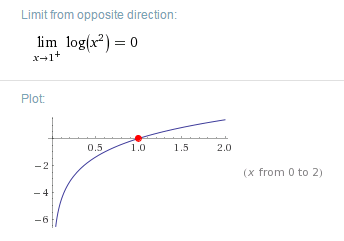
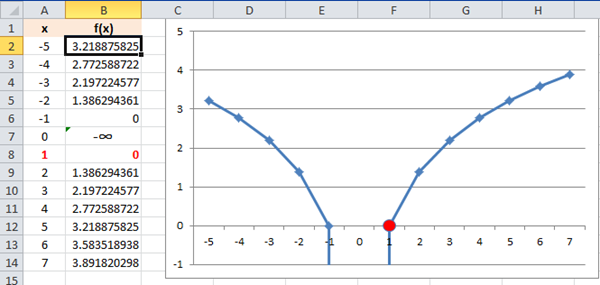
3.- Con cada una de las siguientes funciones tabula y gráfica, utilizando la herramienta de Excel, con un rango para el eje por de -6 a 6. El resultado obtenido debes copiarlo y pegarlo en el mismo archivo que elaboraste las anteriores funciones:
![]()
![]()
Respuesta de Valero Angel Serrano Mercadal
2
1 respuesta más de otro experto
Respuesta
5