Hallar el volumen V del cono
Un cono está circunscrito a una esfera de radio R. Hallar el volumen V del cono como una función de la única variable h, la altura del cono, es decir, hallar V=V(h). Calcule el dominio de esta función.
2 respuestas
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Luis Alberto!
No será solo una función de h sino también de R ya que no nos dan un radio concreto.
Dibujare la proyección de la figura sobre la pared del fondo.
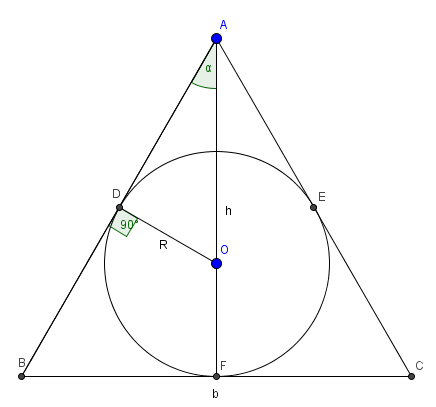
El volumen del cono será:
$$\begin{align}&V=\frac{1}{3}\pi \left(\frac b2\right)^2h\\&\\&\text{debemos poner b como función de h y R}\\&\\&\text{Los triángulos ABF y AOD son semejantes, ya}\\&\text{que son rectágulos y tienen el ángulo }\alpha\text{ común}\\&\text{Por lo tanto}\\&\\&\frac{\overline{AB}}{\overline{AO}}=\frac{\overline{BF}}{\overline{OD}}=\frac{\overline{AF}}{\overline{AD}}\\&\\&\text{nos interesa la segunda igualdad}\\&\\&\frac{\overline{BF}}{\overline{OD}}=\frac{\overline{AF}}{\overline{AD}}\\&\\&\frac{\frac{b}{2}}{R}=\frac h{\overline {AD}}\\&\\&\overline{AD}\; \text{ lo podemos calcular por Pitágoras}\\&\\&\overline{AD}^2+R^2=(h-R)^2\\&\\&\overline{AD}= \sqrt{h^2-2hR+R^2-R^2}= \sqrt{h^2-2hR}\\&\\&\frac{\frac{b}{2}}{R}=\frac h{ \sqrt{h^2-2hR}}\\&\\&\frac b2= \frac{hR}{\sqrt{h^2-2hR}}= \frac{R \sqrt h}{\sqrt{h-2R}}\\&\\&\text{Con lo cual}\\&\\&V(h)= \frac 13 \pi·\frac{R^2h}{h-2R}·h= \frac 13·\frac{R^2h^2}{h-2R}\\&\\&\text{La restricción debe ser que el volumen sea positivo}\\&\\&h-2R\gt 0\\&\\&h\gt 2R\\&\\&Dom\, V= (2R ,\infty)\\&\\&\\&\\&\\&\end{align}$$:
: