¿Cómo resolver este problema de geometría?
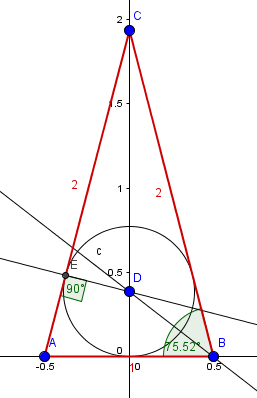
En una pirámide regular cuadrangular, la arista de la base tiene longitud a y las áreas de las caras laterales son iguales al área de la base. Hallar el radio r de la esfera inscrita en la pirámide.
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1