Gráfica la curva correspondiente de la ecuación dada, determinando simetría, dominio, intercepciones, asíntotas

·

·

¡Hola Ale!

Por suerte es una curva donde se puede despejar y

$$\begin{align}&x^2+2xy-5y - 3 = 0\\&\\&2xy-5y = 3-x^2\\&\\&(2x-5)y = 3 - x^2\\&\\&y = \frac{3-x^2}{2x-5}\\&\\&\text{La tabulación te dejo hacerla a tí, toma los puntos}\\&\text{que tengáis por costumbre tomar.}\\&\\&\text{No tiene simetriá par ni impar que son las fáciles de calcular}\\&\\&Dom f= \mathbb R-\left\{\frac 52 \right \}\\&\\&\text{Las intercepciones on el eje X son}\\&\\&3-x^2=0\\&\\&x^2=3\\&\\&x=\pm \sqrt 3\\&\\&\text{con el eje Y es}\\&\\&y =-\frac 3 5\\&\\&\text{Tiene una asíntota vertical en }x= \frac 52\\&\\&\text{Y tiene asíntota oblicua porque}\\&\\&m=\lim_{x\to \infty}\frac{\frac{3-x^2}{2x-5}}{x}=\lim_{x\to \infty}\frac{3-x^2}{2x^2-5x}=-\frac 12\\&\\&b=\lim_{x\to \infty}\frac{3-x^2}{2x-5}- \left(-\frac 12  \right)x=\\&\\&\lim_{x\to \infty}\frac{3-x^2}{2x-5}+\frac x2 =\lim_{x\to \infty}\frac{6-2x^2+2x^2-5x}{4x-10}=-\frac 54\\&\\&\text{luego la asíntota oblicua es}\\&\\&y=-\frac x2-\frac 54\end{align}$$

Todo esto se merece que lo comprobemos:

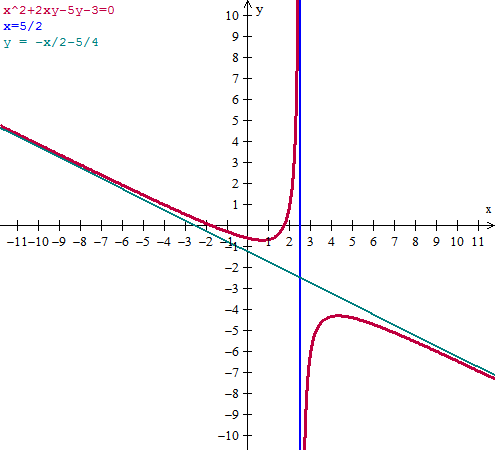
Ahora es cuando se puede ver que la curva es una hipérbola y tiene una simetría central respecto al centro que es

x=5/2

y=-x/2 - 5/4 = -5/4 - 5/4 = -10/4 = -5/2

Luego se simétrica central respecto al punto (5/2, -5/2) lo comprobamos desplazando la curva

$$\begin{align}&y = \frac{3-x^2}{2x-5}\\&\\&y - \frac 52= \frac{3-\left(x+\frac 52  \right)^2}{2\left(x+\frac 52  \right)-5}=\\&\\&y = \frac 52+\frac{3-x^2-5x-\frac {25}4}{2x}=\frac{5x+3-x^2-5x-\frac {25}{4}}{2x}=\\&\\&\frac{-x^2-\frac {13}{4}}{2x}\\&\\&\text{que es impar ya que}\\&\\&f(-x) = \frac{-x^2- \frac {13}4}{-2x}= -f(x)\end{align}$$

Pero bueno, esto último que he hecho a lo mejor no lo habéis dado, en ese caso no lo pongas.

Y eso es todo, sa lu dos.

:

: