¿Cómo resuelvo esta suma de Riemman?

·

·

¡Hola JB Tech!

Te dicen todo lo el cálculo que debes hacer es fácil.

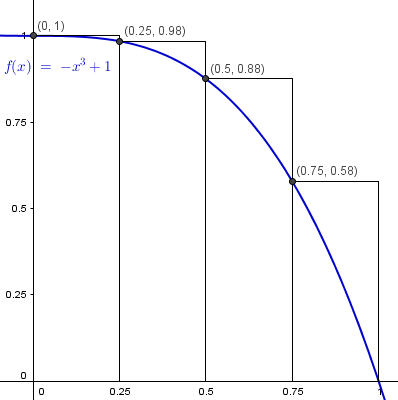
$$\begin{align}&R(f,4)=f(x_0)(x_1-x_0)+f(x_1)(x_2-x_1)+f(x_2)(x_3-x_2)+f(x_3)(x_4-x_3)=\\&\\&\text {hacemos cálculos aparte}\\&\\&f(x_0)=f(0) = -0^3+1=1\\&f(x_1)= f\left(\frac 14  \right)=-\frac 1{64}+1=\frac{63}{64}\\&f(x_2)=f\left(\frac 12  \right)=-\frac{1}{8}+1=\frac 78\\&f(x_3) = f\left(\frac 34  \right)=-\frac{27}{64}+1=\frac{37}{64}\\&x_1-x_0=\frac 14\\&x_2-x_1=\frac 12 - \frac 14= \frac 14\\&x_3-x_2=\frac 34 - \frac 12 = \frac 14\\&x_4-x_3=1-\frac 34 = \frac 14\\&\\&\text{Luego la suma de Rieman es}\\&\\&= 1·\frac 14+\frac{63}{64}·\frac 14+\frac{7}{8}·\frac 14+\frac{37}{64}·\frac 14=\\&\\&\frac 14\left(1+\frac{63}{64}+\frac{7}{8}+\frac{37}{64}  \right)=\\&\\&\frac 14·\frac{64+63+56+37}{64}= \frac 14·\frac{220}{64}=\frac{220}{256}=\frac{55}{64}\\&\\&\end{align}$$

Y esta es la gráfica verdadera, en la del dibujo no tienen la misma medida los dos ejes.

Sa lu dos.

:

:

:

: