Cómo se realiza esta comprobación de igualdad de triángulos?
Demuestra que dos triángulos son iguales si tienen respectivamente un lado y los ángulos adyacentes a este lado
·
·
¡Hola Miguel Angel!
Es el llamado criterio ALA.
Sean ABC y PQR dos triángulos que tienen igual el lado AB = PQ y áng BAC = áng QPR y áng ABC = áng PQR
Por ser congruentes BAC y QPR existe un movimiento combinado de traslación, giro y/o reflexión que transforma el ángulo BAC en el ángulo PQR y se cumple
i) A=P
Ii) La semirrecta AC se transforma en la semirrecta PR
Iii) La semirrecta AB se transforma el la semirrecta PQ
Iv) El punto B se transforma en Q ya que AB=PQ
Sea C' la imagen de de C, tendremos que C' está en la semirrecta PR y áng ABC = ang PQC'
Pero por las premisas tenemos áng ABC=áng PQR y por la propiedad transitiva áng PQC' = áng PQR
Luego C' coincide con R ya que si no PQC' sería mayor o menor que PQR.
Luego C se transforma en R. Y ya tenemos que los tres vértices de ABC se han transformado en los tres de PQR, por lo tanto son dos triángulos congruentes.
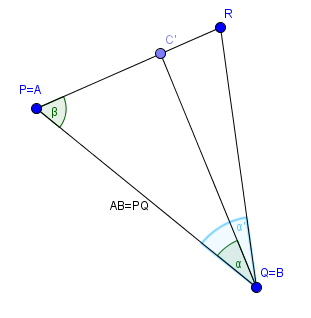
En la imagen se ve eso, al estar C' sobre la semirrecta PR debe ser R para que los ángulos PQC' y PQR sean congruentes tal como dicen las deducciones a las que hemos llegado.
Y eso es todo, saludos.
:
:
