Calcular el flujo del vector a través de una figura cilíndrica
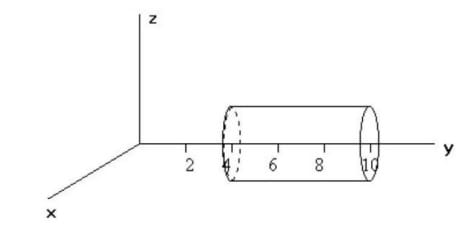
De la figura
Calcular el flujo del vector F=2yj a través de la superficie cilíndrica
De radio unidad de la figura, del cual por lo que puedo observar el radio es =1
·
·
¡Hola Victor!
Lo hacemos sin teoremas, para calcular el flujo considerarás tres superficies, la tapa izquierda, la tapa derecha y la superficie del cilindro.
El flujo es F = 2y j es un vector paralelo al eje Y luego forma 90º con la superficie del cilindro y el flujo a través de esa superficie es 0
En la tapa izquierda por cualquier punto el flujo
F = 2 · 4 j= 8j
El vector normal a la superficie tiene orientación -j y su valor es la superficie de la tapa que es pi, luego el vector superficie es
S = - pi j
Por tanto el flujo en la tapa izquierda
Flujo izda = 8j · (-pi j) = -8pi
En la tapa derecha el vector flujo es:
F = 2 · 10 j = 20 j
y el vector superficie tiene la orientación j, el vector superficie es:
S = pi j
Luego el flujo es
Flujo dcha = 20 j · pi j = 20pi
Por lo tanto el flujo es la suma de los dos
Flujo = -8 pi + 20 pi = 12pi = 37.69911184
Y eso es todo, saludos.
:
:
1 respuesta más de otro experto
Según la orientación mostrada de la superficie cilíndrica, el vector F solo atraviesa las caras laterales.( Bases).
Flujo F = Integral Cerrada ( F . ds) ... que se demuestra que es equivalente a Integral cerrada ( div.F Dv) por el Teorema de Gauss.
Luego div F = d/dy ( Fy) = 2 ..............................Luego Flujo que te piden = 2 Integral ( dv ) entre y=4 e y= 10 ........................................2 pi radio^2 x (10 - 4) = 37.7