Problema de calculo, encontrar el área entre estas dos funciones

·

·

¡Hola JB Tech!

Esta es la gráfica:

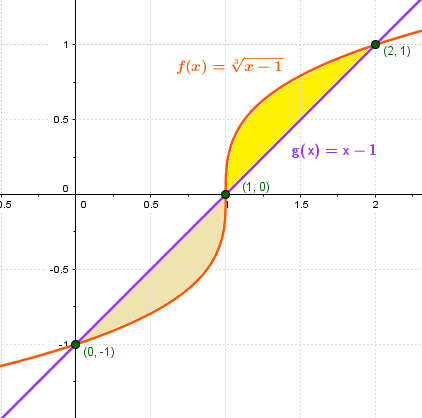
Los puntos de intersección son:

$$\begin{align}&\sqrt[3]{x-1}=x-1\\&\\&x-1= x^3-3x^2+3x-1\\&\\&x^3-3x^2+2x=0\\&\\&x_1=0\\&\\&x^2-3x+2=0\\&\\&(x-1)(x-2)=0\\&\\&x_2=1\\&x_3=2\end{align}$$

Sería interesantísimo comprobar que las funciones son simétricas respecto el punto (1,0)  ya que así bastaría calcular la primera área y multiplicar por 2.

Las funciones desplazadas hacia la izquierda una unidad serían:

$$\begin{align}&f(x+1) = \sqrt[3]{(x+1)-1}= \sqrt[3]x\\&g(x+1)=(x+1)-1=x\\&\\&\text{Y ambas son funciones impares}\\&\\&\sqrt[3]{-x}=- \sqrt[3]x\\&-x = -x\\&\\&\text{Luego desplazadas son simétricas respecto (0,0)}\\&\text{por lo que si}\text{n desplazar son simetricas respecto (1,0)}\\&\\&A=2\int_0^1 [x-1- \sqrt[3]{x-1}]dx=\\&\\&2\int_0^1\left(x-1-(x-1)^{\frac 13}\right)dx=\\&\\&2\left[ \frac{x^2}2-x-\frac{(x-1)^{\frac 43}}{\frac 43} \right]_0^1=\\&\\&2\left(\frac 12-1  -0-0+0+\frac{\sqrt[3]{(-1)^4}}{\frac 43}\right)=\\&\\&2 \left(-\frac 12+\frac 34  \right)=2·\frac{-2+3}{4}=\frac 24 = \frac 12\end{align}$$

Y eso es todo, sa lu dos.

:

: