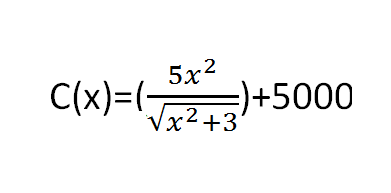Como puedo resolver la siguiente derivada

·

·

¡Hola Aaron Daniel!

Efectivamente, el costo marginal es la derivada. Hay que saber unas pocas reglas de derivación, doy por supuesto que sabes la derivadas de la suma, del producto por una constante y de un monomio. Y doy por supuesto que sabes como se usa la regla de la cadena. Estas son las reglas:

$$\begin{align}&\left(  \frac fg\right)'=\frac{f'g-fg'}{g^2}\\&\\&(\sqrt x)'=\frac{1}{2 \sqrt x}\\&\\&(f[g(x)])'=f'[g(x)]·g'(x)\\&\\&\\&C(x)= \frac{5x^2}{\sqrt{x^2+3}}+ 5000\\&\\&C'(x)=\frac{10x \sqrt{x^2+3}-5x^2·\frac{1}{2 \sqrt{x^2+3}}·2x}{x^2+3}+0=\\&\\&\frac{10x \sqrt{x^2+3}-\frac{5x^3}{\sqrt{x^2+3}}}{x^2+3}=\\&\\&\frac{10x(x^2+3)-5x^3}{(x^2+3) \sqrt{x^2+3}}=\\&\\&\frac{10x^3+30x-5x^3}{(x^2+3) \sqrt{x^2+3}}=  \frac{5x^3+30x}{ \sqrt{(x^2+3)^3}}\\&\end{align}$$

Y eso es todo, sa lu dos.

:

: