Evaluar esta integral, es de sólidos de revolución.

·

·

¡Hola JB!

Este yo creo que sí necesita la gráfica.

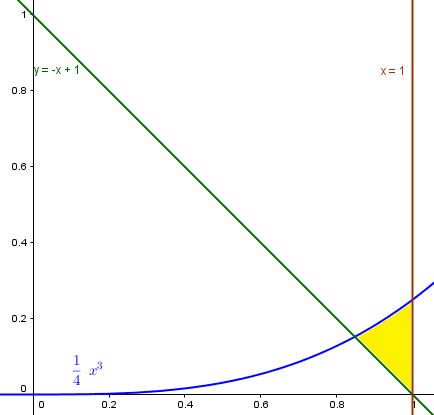
Esta vez creo que será mucho mejor usar el método de los cascarones.

Los limites de integración son el punto de intersección de la azul y la verde y 1

$$\begin{align}&\frac 14 x^3=1-x\\&\\&\text{Se han pasado de rosca, la respuesta que da}\\&\text{WolframAlpha es}\\&x=0.84770756\\&\\&\text{Dadas dos funciones f(x) y g(x) con }f(x)>g(x)\\&\text{Y un intervalo [a,b] con }a\ge0\\&\text{el volumen por cascarones es}\\&\\&V=2\pi\int_a^b x[f(x)-g(x)]dx\\&\\&V= 2\pi \int_{0.84770756}^1 x\left(\frac 14 x^3-(1-x)  \right)dx=\\&\\& 2\pi\int_{0.84770756}^1 \left(\frac 14 x^4-x+x^2  \right)dx=\\&\\&2\pi\left[ \frac 1{20}x^5-\frac {x^2}2+\frac {x^3}3 \right]_{0.84770756}^1=\\&\\&2\pi\left(\frac 1{20}-\frac 12+\frac 13-\frac{0.84770756^5}{20}+\frac{0.84770756^2}{2}-\frac{0.84770756^3}{3}  \right)=\\&\\&0.03538634118\pi=0.11116946948851 \,u^3\\&\\&\\&\end{align}$$

Y eso es todo, saludos.

:

: