Resolver ejercicios de indentidades trigonometicas
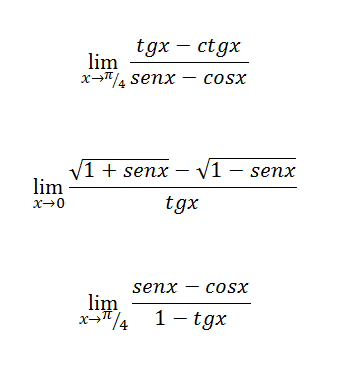
Metodo facil para resolver estos ejeccios de indentidades trigomentica
3 Respuestas
;)
Hola Daniel Rata!
Te contesto aquí dos, y en la otra pregunta el otro.
Como nuevo en el foro te recuerdo que has de votar las respuestas.
En matemáticas, votar Excelente te asegurará nuevas respuestas.
$$\begin{align}&\lim_{x\to \pi/4}\frac{tanx-cotx}{senx-cosx}=\frac{1-1}{\frac{\sqrt 2}{2}-\frac{\sqrt{2}}{2}}=\frac{0}{0}=\\&\\&\lim_{x \to \frac {\pi}{4}}\frac{\frac{senx}{cosx}-\frac{cosx}{senx}}{senx-cosx}=\lim_{x \to \frac {\pi}{4}} \frac{\frac{sen^2x-\cos^2x}{senxcosx}}{senx-cosx}=\lim_{x \to \frac {\pi}{4}}\frac{(senx+cosx)(senx-cosx)}{senxcosx(senx-cosx)}=\\&\\&\lim_{x \to \frac {\pi}{4}}\frac{senx+cosx}{senxcosx}=\frac{\frac{\sqrt 2}{2}+\frac{\sqrt 2}{2}}{\frac{\sqrt 2}{2} \frac {\sqrt 2}{2}}=\\&\\&\frac{\sqrt 2}{\frac{2}{4}}= 2 \sqrt 2\\&\\&\\&\\&3.-\\&\\&\lim_{x \to \frac {\pi}{4}} \frac{senx-cosx}{1-tanx}=\frac{\frac{ \sqrt 2}{2}- \frac {\sqrt 2}{2}}{1-1}=\frac{0}{0}=\lim_{x \to \frac {\pi}{4}} \frac{senx-cosx}{1- \frac{senx}{cosx}}=\lim_{x \to \frac {\pi}{4}} \frac{senx-cosx}{\frac{cosx-senx}{cosx}}=\\&\\&\lim_{x \to \frac {\pi}{4}}(-cosx)=- \frac{ \sqrt 2}{2}\end{align}$$Espero que te sirva y que lo entiendas, sino preguntamé
Saludos
;)
;)
Veo que has mandado dos veces la pregunta, te contestaré aquí el que falta
$$\begin{align}&\lim_{x\to 0} \frac{\sqrt{1+sen x} - \sqrt {1-senx}}{tgx}= \frac{\sqrt{1+0}-\sqrt{1-0}}{0}= \frac 00\\&\\&\text{multiplicamos por el conjugado del numerador}\\&\\&= \lim_{x\to 0} \frac{(\sqrt{1+sen x} - \sqrt {1-senx})·(\sqrt{1+sen x} + \sqrt {1-senx})}{tgx·(\sqrt{1+sen x} + \sqrt {1-senx})}=\\&\\&\lim_{x\to 0} \frac{(\sqrt{1+senx})^2-(\sqrt{1-senx})^2}{tgx·(\sqrt{1+sen x} + \sqrt {1-senx})}=\\&\\&\lim_{x\to 0} \frac{1+senx-(1-senx)}{tgx·(\sqrt{1+sen x} + \sqrt {1-senx})}=\\&\\&\lim_{x\to 0} \frac{2sen x}{tgx·(\sqrt{1+sen x} + \sqrt {1-senx})}=\\&\\&\text{Sigue siendo 0/0, pero si ponemos la tangente como seno/coseno}\\&\\&\lim_{x\to 0} \frac{2sen x}{\frac {senx}{cosx}·(\sqrt{1+sen x} + \sqrt {1-senx})}=\\&\\&\lim_{x\to 0} \frac{2}{\frac {1}{cosx}·(\sqrt{1+sen x} + \sqrt {1-senx})}=\\&\\& \frac{2}{\frac 11·(\sqrt{1+0}+ \sqrt{1-0})}= \frac 2{1(1+1)}= \frac 22 = 1\end{align}$$Y eso es todo, no olvides valorar las respuestas.
Saludos.
:
:
¡Gracias! Si me ayudo para resolerlo, y por primero pensaba que no se publico por eso lo envíe dos veves
Como ya te decía en la otr respuesta, debes votar excelente, tu no querrías que en un examen de 10 te pusieran un 5, pues lo mismo nosotros. Puedes subir la nota debajo de cada respuesta pinchando donde pone Votada.
Sa lu dos.
