Como resuelvo estos ejercicios e integración de volúmenes
Estos ejercicios son de aproximación e integración de volúmenes.
- Un solido semicircular acotada por
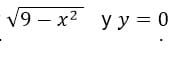Tiene secciones transversales perpendiculares al eje por que son cuadrados. Encuentre el volumen de este solido. - Determine el volumen del solido de revolucion generado al hacer girar la region R acotada por la recta
$$\begin{align}&y=4x\end{align}$$y la parabola$$\begin{align}&y=x^2\end{align}$$Alrededor del eje x.
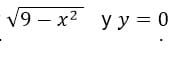Tiene secciones transversales perpendiculares al eje por que son cuadrados. Encuentre el volumen de este solido.1 Respuesta
·
·
¡Hola JB Tech!
Nunca más de un ejercicio de de estos por pregunta, además el primero tiene miga.
No haré el dibujo, es muy sencillo, es el semicírculo superior de una circunferencia centrada en el origen de radio 3.
Nos dicen que las secciones transversales son cuadrados, cada cuadrado será más o menos grande dependiendo de la posición, por ejemplo en los extremos son cuadrados de lado 0 y el el medio el lado es 3.
En cada punto x el lado mide raíz(9-x^2)
Luego el área del cuadrado sera
A(x) = 9 -x^2
Y el volumen es la integral de todas las áreas de los cuadrados
$$\begin{align}&V=\int_{-3}^3(9-x^2)dx =\left[9x - \frac {x^3}3 \right]_{-3}^3=\\&\\&27 - 9+27-9 = 36\; u^3\end{align}$$Y eso es todo, saludos.
:
:
