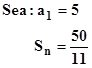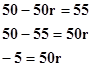Planteamiento a problema de progresiones aritméticas y geométricas
Agradezco su colaboración con la solución del siguiente problema
Respuesta de Luis Alberto Candio Salcedo
2
Como estas Fabiancho:
Te resuelvo el ejercicio, pero con una observación: la pregunta deber ser: ¿Cuál debe ser la razón para que la suma de términos infinitos sea 50/11?
Luego:
Tenemos la fórmula:
Reemplazamos:
Resolvemos:
Finalmente:
Listo. Eso es todo, espero que puedas entender. No te olvides puntuar la respuesta para seguir gozando de nuevas respuestas,...
1 respuesta más de otro experto
Respuesta de Lucas m
1
;)
Hola fabiancho!
$$\begin{align}&S_n=\frac{a_nr-a_1}{r-1}=\frac{a_1r^{n-1}r-a_1}{r-1}=a_1 \frac{r^n-1}{r-1}\\&\\&\frac{50}{11}=5 \frac{r^n-1}{r-1}\\&\\&\frac{10}{11}= \frac{r^n-1}{r-1}\\&\\&Si \ n=2\\&\\&\frac{10}{11}= \frac{r^2-1}{r-1}=r+1 \Rightarrow r=\frac{10}{11}-1=\frac{-1}{11}\\&\\&Si \ n=3\\&\frac{10}{11}= \frac{r^3-1}{r-1}=r^2+r+1 \Rightarrow 11r^2+11r+11=10 \\&\\&11r^2+11r+1=0 \Rightarrow r=\frac{-11 \pm \sqrt {77}}{22}\\&\\&Si \ n=4\\&\\&\frac{10}{11}= \frac{r^4-1}{r-1}=r^3+r^2+r+1 \Rightarrow 11r^3+11r^2+11r+1=0\\&\\&\\&Si \ n=5 \Rightarrow11r^4+11r^3+11r^2+11r+1=0\\&\\&Si \ n=k \Rightarrow 11r^{k-1}+11r^{k-2}+·······+11r+1=0\end{align}$$Saludos
;)
;)