F(x) = x3 + 4x2 – 10 tiene una raíz en [1, 2] y utilizando el Método de bisección determine una aproximación a

·

·

¡Hola Luk!

Con un poco de suerte supongo que habrán puesto dos puntos donde los valores de la función sean de distinto signo

F(1) = 1^3 + 4·1^2 - 10 = 1+4-10 = -5

F(2) = 2^3 + 4·2^2 -10 = 8 + 16 -10 = 14

Vale, son de distinto signo y la función es continua en [1, 2] por el teorema de Bolzano habrá al menos una raíz.

Tomaremos el valor medio y calculamos la función

c_0 = (a_0+b_0) / 2 = (1+2)/2 = 1.5

F(1.5) = 1.5^3 + 4 · 1.5^2 - 10 = 2.375 > 0.001

Para que los signos de los valores de la función en los extremos sean distintos tomamos

[a_1, b_1] = [1, 1.5]

c_1 = [1+1.5] / 2 = 1.25

f(1.25) = 1.25^3 + 4 · 1.25^2 - 10 = -1.796875 < -0.001

Ahora se debe tomar [1.25, 1.5]  ya que F(1.25)<0 y F(1.5)>0

[a_2, b_2] = [1.25, 1.5]

c_2 = (1.25+1.5)/2 = 1.375

F(1.375) = 1.375^3 + 4 · 1.375^2 - 10 = 0.162109375 >0.001

Ahora se debe tomar

[a_3, b_3] = [1.25, 1.375]

c_3 = (1.25+1.375) = 1.3125

F(1.3125) = 1.3125^3 + 4 · 1.3125^2 - 10 = -0.8483886719 <-0.001

Y así rato y rato porque este método converge muy lentamente, así que vamos a preparar la hoja de Excel. La elección de intervalos la haré por producto de valores, de modo que la hoja te servirá igual para situaciones -+ como +-

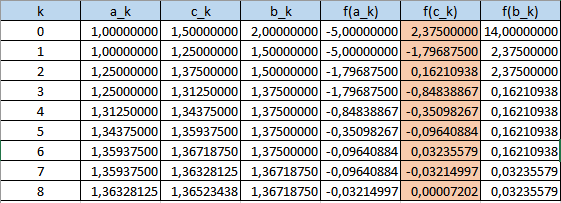
Que el primer c sea c_0 lo he tomado de la Wikipedia, yo lo hubiera llamado más bien c_1 porque indica el valor que se prueba en la primera iteración, pero por no llevar la contraria lo dejé así.

Y aquí tienes la última versión de la hoja de Cálculo: Hoja de calcular raíces numéricamente, tres métodos.

Y eso es todo, sa lu dos.

:

: