Limites al infinito de la siguiente función
Aplicando los limites al infinito demuestra los limites de las siguientes funciones.
Hola un amigo mio se podía hacer con binomios conjugados no se si se refería a que multiplicara :
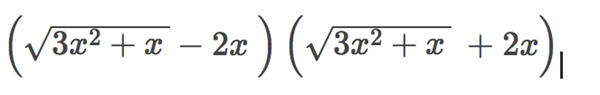
O ¿cuál es el procedimiento que recomiendan a seguir?
·
·
¡Hola Misael!
Este tipo de límites no se concibe resolverlos de otra forma que no sea multiplicando y dividiendo por el conjugado. No obstante hay algunos en los que quitando los términos de menor peso se pueden resolver. Pero hay que tener algo de cuidado con este método
$$\begin{align}&\lim_{x\to \infty} ( \sqrt{3x^2+x}-2x) =\\&\\&\lim_{x\to\infty}(\sqrt{3x^2}-2x)=\\&\\&\lim_{x\to \infty}(\sqrt 3\;x-2x)=\\&\\&\lim_{x\to \infty} x(\sqrt 3-2)=\\&\\&\lim_{x\to \infty} -0.267949 x= -\infty\end{align}$$Y si se quiere hacer sin usar para nada lo de los términos de más peso sería así.
$$\begin{align}&\lim_{x\to \infty} ( \sqrt{3x^2+x}-2x) =\\&\\&\lim_{x\to \infty} ( \sqrt{3x^2+x}-2x) · \frac{ \sqrt{3x^2+x}+2x}{ \sqrt{3x^2+x}+2x}=\\&\\&\lim_{x\to \infty} \frac{3x^2+x-4x^2}{\sqrt{3x^2+x}+2x}=\\&\\&\lim_{x\to \infty} \frac{-x^2+x}{\sqrt{3x^2+x}+2x}=\\&\\&\text{dividimos todo entre x}\\&\\&\lim_{x\to \infty} \frac{-x+1}{\frac{\sqrt{3x^2+x}}{x}+2}=\\&\\&\lim_{x\to \infty} \frac{-x+1}{\sqrt \frac{{3x^2+x}}{x^2}+2}=\\&\\&\lim_{x\to \infty} \frac{-x+1}{\sqrt {3+\frac{1}{x}}+2}=\frac{-\infty+1}{\sqrt 3+2}= -\infty\end{align}$$Y eso es todo, sa lu dos.
:
:
1 respuesta más de otro experto
;)
Hola Misael Landero!
Es una indeterminación infinito -infinito; que a veces se resuelven operando, cosa que no se puede hacer cuando hay un radical por medio. Entonces se multiplica y divide la expresiónpor su binomio conjugado, y así poder aplicar la identidad notable:
$$\begin{align}&(A+B)(A-B)=A^2-B^2\\&\\&\lim_{x \to +\infty} ( \sqrt {3x^2+x}-2x)= \infty-\infty=\\&\\&\lim_{x \to +\infty} ( \sqrt {3x^2+x}-2x)· \frac{ ( \sqrt {3x^2+x}+2x)}{ ( \sqrt {3x^2+x}+2x)}=\\&\\&\lim_{x \to +\infty} \frac{( \sqrt {3x^2+x})^2-(2x)^2}{( \sqrt {3x^2+x}+2x)}=\\&\\&\lim_{x \to +\infty} \frac{ {3x^2+x}-4x^2}{ \sqrt {3x^2+x}+2x}= \\&\\&\lim_{x \to +\infty} \frac{ {-x^2+x}}{ \sqrt {3x^2+x}+2x}=\frac{- \infty}{+\infty}= términos \ dominantes=\\&\\&\lim_{x \to +\infty} \frac{-x^2}{ \sqrt {3x^2}+2x}= \lim_{x \to +\infty} \frac{-x^2}{(\sqrt 3 +2)x}= \frac{1}{\sqrt 3 +2} \lim_{x \to +\infty} \frac{-x^2}{x}=\\&\\&\frac{1}{\sqrt 3 +2} \lim_{x \to +\infty} (-x)= -\infty\end{align}$$Hay que coger los términos dominantes del numerador y denominador.
El del numerador es el de grado 2 (3x^2)
El del denominador son los de grado 1:
$$\begin{align}&\sqrt{3x^2}+2x\end{align}$$un término de grado 2 en una raíz cuadrada equivale a un término de grado uno.
Saludos
;)
;)