Demostrar el limite de la siguiente función

·

·

¡Hola Misael!

Grafícando solo te puedes hacer una idea en caso de que tienda a algún número corriente, se tiene que hacer analíticamente y luego si quieres compruebas graficando.

$$\begin{align}&\text{sabemos que}\\&\\&a^3-b^3=(a-b)(a^2+ab+b^2)\\&\\&a-b= \frac{a^3-b^3}{a^2+ab+b^2}\\&\\&\text{Si llamamos}\\&\\&a= (x^3+x)^{\frac 13}\\&\\&b= (x^3+1)^{\frac 13}\\&\\&\text{tendremos}\\&\\& (x^3+x)^{\frac 13}-(x^3+1)^{\frac 13} = \frac{x^3+x-x^3-1}{(x^3+x)^{\frac 23}+(x^3+x)^{\frac 13}(x^3+1)^{\frac 13}+(x^3+1)^{\frac 23}}=\\&\\&\frac{x+1}{(x^3+x)^{\frac 23}+(x^3+x)^{\frac 13}(x^3+1)^{\frac 13}+(x^3+1)^{\frac 23}}=\\&\\&\text{Al tomar límites en el infinito se puede prescindir de los de menos grado}\\&\\&\lim_{x\to -\infty}\frac{x+1}{(x^3)^{\frac 23}+(x^3)^{\frac 13}(x^3)^{\frac 13}+(x^3)^{\frac 23}}=\\&\\&\lim_{x\to -\infty}\frac{x+1}{x^2+x^2+x^2}=\lim_{x\to -\infty}\frac{x+1}{3x^2}=\\&\\&\text{dividiendo todo por }x^2\\&\\&\lim_{x\to \infty} \frac{\frac 1x +\frac 1{x^2}}{3}=\frac{ 0+0}3=0\end{align}$$

Y la gráfica distorsionada para que se vea más claro el límite es esta:

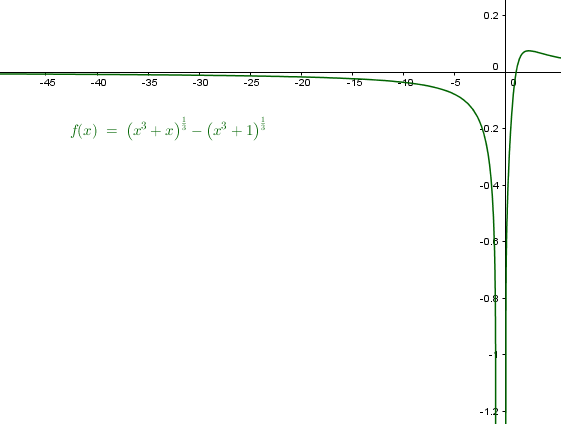
Que corrobora lo calculado.

Y eso es todo, saludos.

:

: