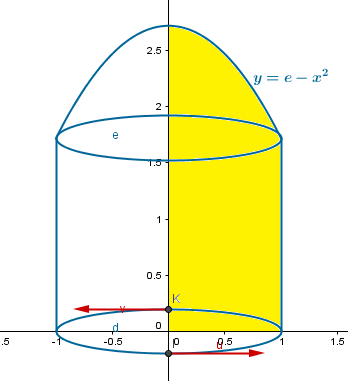
Encuentre el volumen generado al rotar la región
Por favor encuentre el volumen generado al rotar la región limitada por y = ex2,
y = 0, x = 1 al rededor del eje y dibuje el solido obtenido.
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Flover!
No conozco ningún buen programa que haga gráficas tridimensionales de regiones girando, usaré Geogebra y pondré la perspectiva por mi cuenta.
El procedimiento más rápido en este caso será el de los cascarones cilíndricos. Dados dos puntos
$$\begin{align}&0\le a\le b\\&\\&\text{y una función f(x), el volumen entre el eje X y la función}\\&\text{girando alrededor del eje Y entre a y b es}\\&\\&V=\int_a^b x·f(x)dx=\\&\\&\int_0^1 x(e-x^2)dx= \int_0^1(ex-x^3)dx=\\&\\&\left[\frac{ex^2}{2}-\frac {x^4}4 \right]_0^1= \frac e2- \frac 14\end{align}$$Y eso es todo, sa lu dos.
:
:
