Calcular la simetría de las siguientes funciones

;)
Hola Elkin Campos!

Una función es simétrica respecto al eje de ordenadas(Y), llamadas funciones pares, si

f(x)=f(-x) (la imagen de x y de sus opuestos son iguales). Vamos que si doblas el papel por el eje y, se superpone lo de un lado y lo del otro.

Una función es simétrica respecto el Origen de coordenadas, llamadas funciones impares, si cumple f(-x)=-f(x).

$$\begin{align}&a)\\&f(x)=3x^3-5x^2-5x+16\\&f(-x)=3(-x)^3-5(-x)^2-5(-x)+16=-3x^3-5x^2+5x+16\\&f(-x) \neq f(x)\\&No \ Par\\&\\&-f(x)=-(3x^3-5x^2-5x+16)=-3x^3+5x^2+5x-16\\&f(-x) \neq -f(x)\\&No \ impar\\&\\&no simétrica\\&b)\\&g(x)=25x^5-12x^4+3x^3+15x\\&g(-x)=-25x^5-12x^4-3x^3-15x\\&g(-x) \neq g(x)\\&no \ par\\&-g(x)=-(25x^5-12x^4+3x^3+15x)=-25x^5+12x^4-3x^3-15x\\&g(-x) \neq -g(x)\\&no \ impar\\&\Rightarrow\\&no \ simétrica\\&\\&c)\\&h(x)=\frac{7x^2-16x+1}{x^3+12x^2-11x}\\&\\&h(-x)=\frac{7x^2+16x+1}{-x^3+12x^2+11x}\\&\\&h(-x) \neq h(x)\\&no \ par\\&-h(x)=-\frac{7x^2-16x+1}{x^3+12x^2-11x}\\&\\&h(-x) \neq -h(x)\\&No \ impar\\&\\&d)\\& l(x) =2x^2-16\\&l(-x)=2(-x)^2-16=2x^2-16\\&l(-x)=l(x)\\&Par \Rightarrow simétrica \ respecto \ eje Y\end{align}$$

a)

b)

c)

4)

Saludos

;)

;)

·

·

¡Hola Elkin!

Yo no sé hasta que punto habéis avanzado en el tema este de la simetría.

Básicamente se habla de dos tipos de simetría.

Simetría axial respecto del eje Y, también llamada par. Son las funciones que cumplen

f(-x) = f(x)

Si son polinomios se caraterizan porque todos los términos son de grado par, el termino independiente también sirve.

·

Simetría central respecto al punto (0,0) también llamada impar. Son las funciones que cumplen

f(-x) = - f(x)

Y si la función es un polinomio tiene todos los términos de grado impar.

·

Luego podría hablarse de simetría respecto de cualquier eje vertical, por ejemplo todas las parábolas son simétricas respecto del eje longitudinal, que pasa por el vértice.

Y también podría haber simetría central respecto de otro punto distinto de (0,0)

Pero estos dos casos ya no son tan sencillos de calcular, por eso te preguntaba hasta que nivel habéis llegado.

·

Vamos a ver que puede hacerse:

Si es un polinomio y hay exponentes pares e impares será simetría par si el grado es par y simetría impar si el grado es impar.

Es por ello que f(x) y g(x) tienen simetría impar

En f(x) veo sencillo calcular el punto sobre el que es simétrica, es el punto de inflexión.

f(x)= 3x^3 - x^2 - 5x + 16

f'(x) = 9x^2 - 2x - 5

f''(x) = 18x - 2

igualando a 0 tenemos

18x -2 = 0

18x = 2

x = 1/9

f(x) = 1/243 - 1/81 - 5/9 + 16 = 3751/243

Luego es simétrica central respecto del punto (1/9, 3761/243)

Aquí puedes descargar el fichero de Goegebra: Fichero Geogebra de f(x)

Y esta es la imagen:

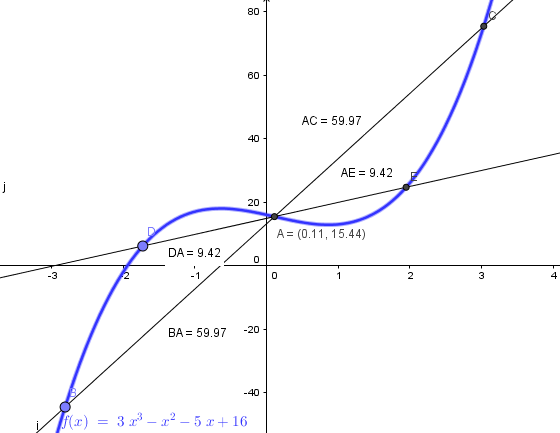
El punto A es e centro de simetría y he trazado dos rectas pasando por él viendo que los cortes equidistan del punto A, lo cual prueba la simetría respecto de A.

No sé si es esto lo que te piden o incluso tú conoces teoría mejor sobre esto. El ejercicio completo me lleva mucho trabajo, deberás mandarlas de una y confirmarme si es así como debe hacerse.

Sa lu dos.

:

.