Para la función dada determine la solución real del respectivo dominio y rango y compruebe con Geogebra:

·

·

¡Hola Oscar!

El dominio serán los puntos donde el radicando es no negativo y el denomindor distinto de 0. Puesto que el denominador es la raíz cuadrada el radicando debe ser estrictamente positivo. Resumiendo el dominio son los puntos donde el radicando es positivo

x-4 > 0

x > 4

Dom f = (4, +infinito)

Y el rango es el dominio de la función inversa.

$$\begin{align}&y=\frac{x-7}{\sqrt{x-4}}\\&\\&y \sqrt{x-4}=x-7\\&\\&y^2(x-4) = x^2-14x+49\\&\\&y^2x-4y^2=x^2-14x+49\\&\\&x^2-14x-y^2x+49+4y^2=0\\&\\&x^2-(14+y^2)x+49+4y^2=0\\&\\&x= \frac{-14-y^2\pm \sqrt{(14+y^2)^2-4(49+4y^2)}}{2}\\&\\&\text{El dominio es donde el radicando es no negativo}\\&\\&196+28y^2+y^4-196-16y^2\ge0\\&\\&y^4+12y^2\ge0\\&\\&y^2(y^2+12)\ge 0\\&\\&y^2 \text{ es siempre positivo}\\&\\&y^2+12\ge0\\&\\&y^2\ge -12\\&\\&\text{Esto sucede siempre}\\&\\&Dom f^{-1]}=\mathbb R\implies Rango f=\mathbb R\end{align}$$

Luego me sale que el rango es todo R, vamos a comprobarlo.

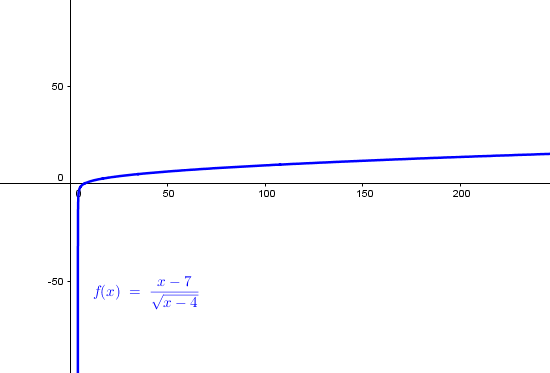
Es una función de crecimiento muy lento, pudiera parecer que se paré en algun momento pero no, el límite en infinito es infinito, luego el rango es todo R.

Y eso es todo, sa lu dos.

:

: