Calcular la simetría de las siguientes funciones y compruebe con Geogebra.
Continuo con mi taller amigos de todo expertos espero su ayuda estoy atento
1 Respuesta
·
·
¡Hola Oscar!
Si nos atenemos a simetría axial sobre el eje Y o simetría central sobre el punto (0,0) no tienen esa simetría ninguna de las dos ya que los polinomios simétricos sobre el eje Y son los que tienen todos los términos con exponente par y los simétricos centrales sobre el punto (0,0) son los que tienen todos sus términos con exponente impar.
Luego No tienen ninguna de esas simetrías estándar.
Ahora bien, un polinómio de grado par puede tener simetría axial sobre cierta recta de la forma x=k. Y un polinomio de grado impar puede tener simetría central sobre un punto (h, k). Determinar esta recta o punto puede ser difícil dependiendo del grado del polinomio.
a) Puede tener simetria central (impar) sobre un punto, tiene que ser un punto de inflexión, luego anulará la derivada segunda
f(x) = x^3 - x^2 - 5x + 16
f'(x) = 3x^2 -2x -5
f''(x) = 6x - 2 = 0
6x=2
x=1/3
f(1/3) = 1/27 - 1/9 - 5/3 + 16 = (1 - 3 - 45 + 432)/27 = 385/27
Luego tiene simetría central sobre el punto (1/3, 385/27)
Y esta es la comprobación:
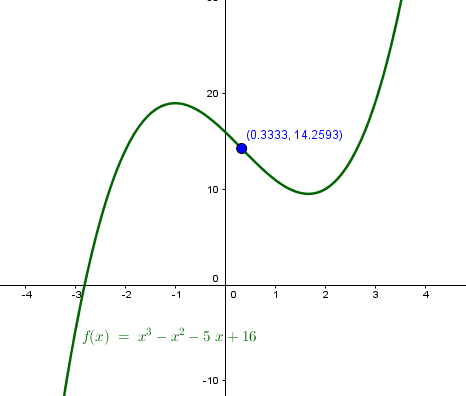
b) Es también simetría impar sobre un punto indeterminado, pero esta vez vamos a ver si lo podemos calcular
g(x) = 25x^5 - 12x^4 + 3x^3 + 15x
g'(x) = 125x^4 - 48x^3 + 9x^2 + 15
g''(x) = 500x^3 - 144x^2 + 18x = 0
Perfecto, una raíz es 0, pero sabemos que esa no puede ser, ya que entonces seria el punto (0, g(0)) = (0,0) que no lo es por tener términos pares.
simplificando x tendremos
500x^2 - 144x + 18 = 0
$$\begin{align}&x= \frac{144\pm \sqrt{20736-36000}}{1000}\end{align}$$No tiene soluciones, luego no hay otra ráiz que 0 que ya sabemos que no sirve, luego no hay simetría. En una primera impresión podría parecer simétrica, pero si calculas:
g(1)=31
g(-1) = -55
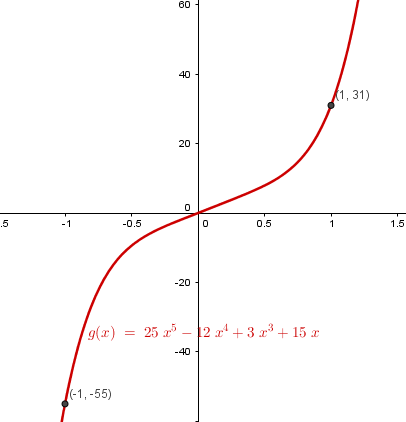
Y eso es todo, espero que te sirva y lo hayas entendido.
Sa lu dos.
:
:
Perdona, transcribí mal la primera función y a partir de ahí todo está mal porque te he resuelto una función distinta
f(x) = 3x^3 - x^2 - 5x + 16
f'(x) = 9x^2 - 2x - 5
f''(x) = 18x - 2 = 0
18x = 2
x=1/9
f(1/9) = 1/243 - 1/81 - 5/9 + 16 = (1-3-135+3888) / 243 = 3751/243
Luego tiene simetria central respecto (1/9, 3751/243)
Bueno, tal vez los medios que usé no estén homologados, se me han ocurrido sobre la marcha, vamos a comprobar que hay esa simetría central.
Si hay simetría central respecto a un punto (h,k) debe cumplirse
f(x+h)-k = k - f(-x+h)
f(x+h)+f(-x+h)=2k
$$\begin{align}&f(x)=3x^3-x^2-5x+16\\&\\&(h,k) = \left(\frac 19,\frac{3751}{243} \right)\\&\\&f\left(x+\frac 19\right)= 3\left(x+\frac 19\right)^3-\left(x+\frac 19\right)^2-5\left(x+\frac 19\right)+16=\\&\\&3x^3+x^2+\frac x{27}+\frac 1{243}-x^2-\frac 29x-\frac 1{81}-5x-\frac 59+16=\\&\\&3x^3-\frac {140}{27}x+\frac {3751}{243}\\&\\&\\&\\&f\left(-x+\frac 19\right)= 3\left(-x+\frac 19\right)^3-\left(-x+\frac 19\right)^2-5\left(-x+\frac 19\right)+16=\\&\\&-3x^3+x^2-\frac x{27}+\frac 1{243}-x^2+\frac 29x-\frac 1{81}+5x-\frac 59+16=\\&\\&-3x^3+\frac {140}{27}x+\frac {3751}{243}\\&\\&\\&f(x+h)+f(-x+h)=\\&\\&3x^3-\frac {140}{27}x+\frac {3751}{243}-3x^3+\frac {140}{27}x+\frac {3751}{243}= 2·\frac {3751}{243}=2k\end{align}$$Luego está bien.
Sa lu dos.
:
:
