Resolver los siguientes ejercicios de simetría y comprobar en geogebra

Ya que hay que graficar, empecemos por el gráfico

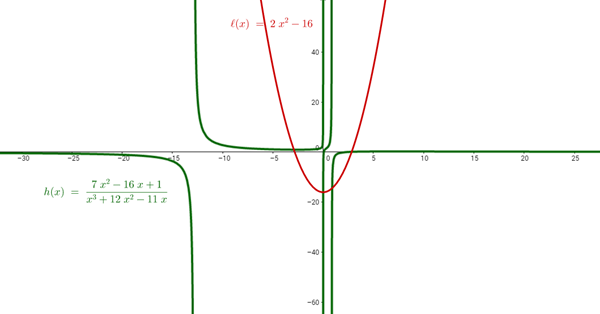
Claramente se ve que h(x) no es nada, y que l(x) es par, veamos si llegamos a la misma conclusión

$$\begin{align}&h(x) \ es\ Par?\\&h(x) = h(-x)\\&h(x) = \frac{7x^2-16x+1}{x^3+12x^2-11x}\\&h(-x) =\frac{7(-x)^2-16(-x)+1}{(-x)^3+12(-x)^2-11(-x)}= \frac{7x^2+16x+1}{-x^3+12x^2+11x}\ne h(x)\\&h(x) \ es\ Impar?\\&-h(x) = h(-x)\\&-h(x) = -\frac{7x^2-16x+1}{x^3+12x^2-11x}\\&h(-x) =\frac{7(-x)^2-16(-x)+1}{(-x)^3+12(-x)^2-11(-x)}= \frac{7x^2+16x+1}{-x^3+12x^2+11x}\ne -h(x)\\&---\\&l(x) \ es\ Par?\\&l(x) = l(-x)\\&l(x) = 2x^2-16\\&l(-x) = 2(-x)^2-16 = 2x^2-16 = l(x) \ SI\\&\text{Al ser par, no hace falta verificar si es impar}\end{align}$$

Salu2