Como se resuelven problemas por el método de Gauss Jordan
En una escuela se desea lleva a cabo un torneo deportivo que abarca tres especialidades: Foot-ball, volleyball y basketball. Se cuenta con 155 alumnos, de los cuales 90 serán titulares y los restantes 65 serán reservas por haber obtenido malas calificaciones; además cada alumno sólo se puede dedicar a una especialidad deportiva. El objetivo es encontrar el número de equipos que se pueden formar en cada deporte. Para cada equipo de football se requieren 11 jugadores titulares y 6 reservas; para cada equipo de volleyball se necesitan 6 titulares y 6 reservas, y para cada equipo de basketball son necesarios 5 titulares y 5 reservas. Encuentre la solución.
1 respuesta
Respuesta de Lucas m
3
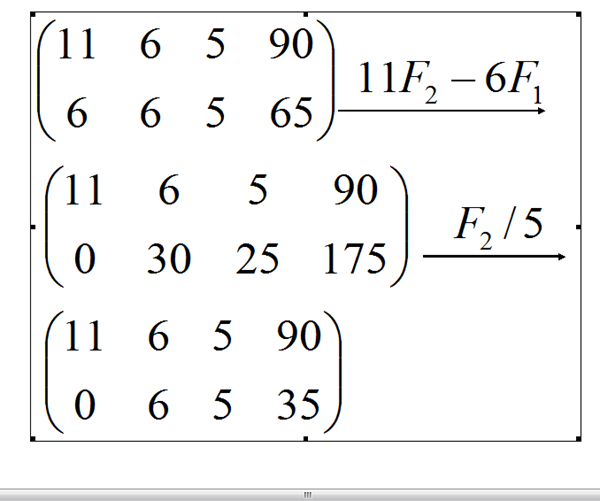

Gracias por asumir el esfuerzo de no escribirlo a mano. Esta respuesta es más clara que la primera. - Hector Orobio Valencia