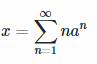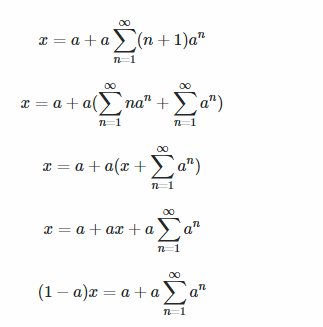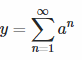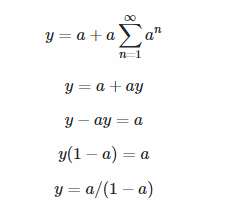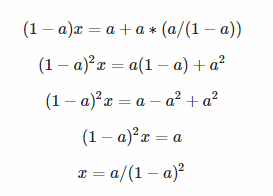Suma infinita de función con exponencial
Alguien me podría explicar cómo calcular
la suma desde x=1 hasta infinito de : x*a^x
Más info: mi "a" será entre 0 y 1.
1 Respuesta
;)
Hola Fran Garsan!
Si x es cualquier Real, no necesariamente entero, entonces yo haría la integral impropia:
$$\begin{align}&\sum_1^{\infty}xa^x= \int_1^{\infty}xa^xdx\\&\\&\int xa^xdx= Por\partes=\\&\\&\\&x=u \Rightarrow du=dx\\&a^x dx=dv \Rightarrow v= \int a^xdx=\frac{a^x}{lna}\\&\\&\int u dv=uv- \int v du\\&\\&=x \frac{a^x}{lna}- \int \frac{a^x}{lna}dx= \frac{xa^x}{lna}- \frac{a^x }{ln^2a}\\&\\&\int_1^{\infty}xa^xdx=\lim_{x \to \infty} \Bigg[\frac{xa^x}{lna}- \frac{a^x }{ln^2a} \Bigg]-\lim_{x \to 1^+} \Bigg[\frac{xa^x}{lna}- \frac{a^x }{ln^2a} \Bigg]=\\&\\&0-\lim_{x \to 1^+} \Bigg[\frac{xa^x}{lna}- \frac{a^x }{ln^2a} \Bigg]=- \Bigg[\frac{a}{lna}-\frac{a}{ln^2a} \Bigg]=\frac{a-a·lna}{ln^2a}= \frac {a(1-lna)}{ln^2a}\\&\\&\end{align}$$Saludos
;)
;)
Gracias por la respuesta,
Disculpa te pego en modo látex para que se entienda mejor el problema.
\sum_{x=1}^\infty x*a^x
Es decir x es entero.
Saludos.
;)
Recuerda que debes votar las respuestas!
Sea:
Trabajamos a parte:
sustituyendo atrás:
Recuerda que debes de votar las respuestas
Muchas gracias por la respuesta.
me ha surgido la duda del primer paso en el que se dice que x=a+a*sum.....
¿de donde sale? No veo que la igualdad sea cierta
Y aunque lo he visto.
Saludos
;)
Si es de sacar factor común a partir del segundo término:
$$\begin{align}&x=\sum_{n=1}^{\infty}n a_n=a+2a^2+3a^3+4a^4+······\\&\\&=a+a \Big(2a+3a^2+4a^3+·····=\\&=a+a \sum_{n=1}^{\infty}(n+1)a^n\end{align}$$;)
