Problema 7. Calcule el valor de Z en el siguiente triangulo, así como cada uno de los ángulos presentes.
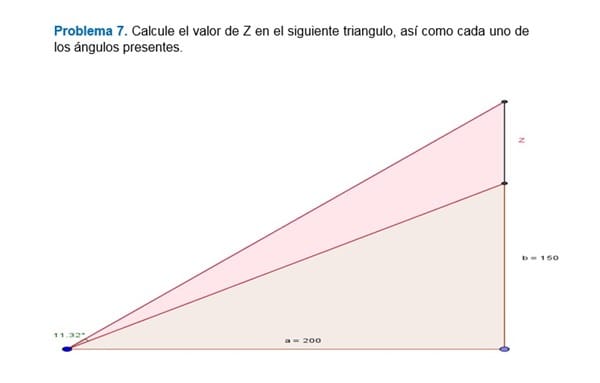
Buenas noches amigos de todo expertos espero me ayuden con este trabajo
3 Respuestas
Respuesta de Kvothe Orwell
1
Respuesta de tmoli
1
Respuesta de Nelsy orozco duque
1

