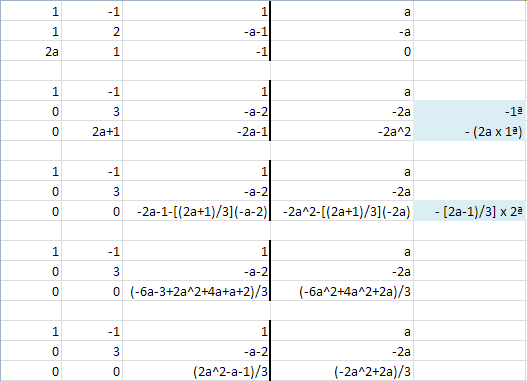Resolución de sistemas de ecuaciones en función de un parámetro por teorema de Rouche.

·

·

¡Hola Juana!

Vamos a hacer las operaciones típicas de fila que se hacen siempre.

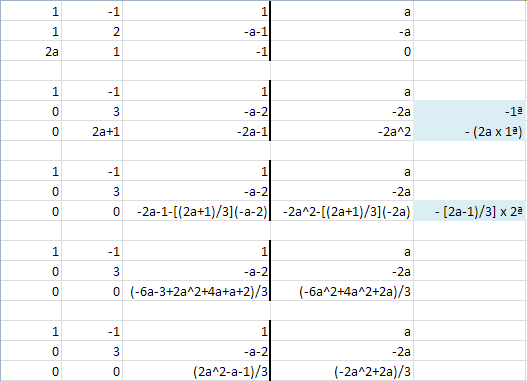
Ahora vamos a ver par que valores de a se hacen cero las celdas de la última fila

En

2a^2 - a -1 = 0

Se ve claramente que si a=1 se cumple, pero la otra raíz no se ve tan fácil, resolveremos la ecuación

$$\begin{align}&a= \frac{1\pm \sqrt{1+8}}{4}=\frac{1\pm 3}{4}=1 \;y\;-\frac 12\\&\\&\\&\text{Y la otra es}\\&\\&-2a^2+2a=0\\&\\&2a(-a+1)=0\\&\\&a=0\, y\;1\\&\\&Si \;a\neq 1 \;y \;a\neq - \frac 12  \quad \text{es compatible determinado}\\&\\&Si \;a=1  \quad\text{es compatible indeterminado con un parámetro}\\&\\&Si \;a=-\frac 12 \quad\text {es incompatible}\end{align}$$

Dentro del caudro de la fórmula se puede escribir poco.

Si a es distinto de 1 y -1/2 la matriz de coeficientes tiene rango 3 (el del número de incógnitas) y entonces la respuesta es única.

Si a = 1 el rango de la matriz de coeficientes y la ampliada es 2 ya que la última fila es todo ceros, luego es compatible indeterminado y el número de parámetros necesarios es 3-2=1

Si a= -1/2 tenemos 0 en el tercer lugar, pero no en el cuarto con lo cual el rango de la matriza de coeficientes es 2 y el de la ampliada es 3 y el sistema es incompatible.

·

Para a=1 ya sabemos que un sistema compatible indeterminado, tomaremos z como parámetro

Sustituyendo a=1 la segunda ecuación queda así:

3y - (-1-2)z = -2·1

-3y +3z = 2

-3y = 2-3z

y = -2/3 + z

Y yendo a la primera

x - (-2/3 + z) +z = 1

x +2/3 -z + z = 1

x+2/3 = 1

x=1/3

Luego la respuesta es

x = 1/3

y = -2/3 + z

z=z

para todo z de R.

·

Y si a= -1 el sistema que queda es

1  -1    1 | -1

0  3    -1 |  2

0  0  2/3| -4/3

z = -2

y +2 = 2  ==>  y=0

x -0 -2 = -1  ==> x = 1

·

Y eso es todo, sa lu dos.

:

: