Problema 2. Demostrar que : 〖2x〗^2-〖4y〗^2+12x+24y+18=0 representa una hipérbola y determine:

;)
Hola omar!
Completando cuadrados:

$$\begin{align}&2x^2-4y^2+12x+24y+18=0\\&\\&2(x^2+6x)-4(y^2-6y)+18=0\\&\\&2(x+3)^2-18-4(y-3)^2+36+18=0\\&\\&2(x+3)^2-4(y-3)^2=-36\\&\\&4(y-3)^2-2(x+3)^2=36\\&\\&dividiendo  \ por \ 36\\&\\&\frac{(y-3)^2}9- \frac{(x+3)^2} {18}=1\\&\\&hipérbola \ con \ eje \ vertical\\&Centro (-3,3)\\&eje \x=-3\\&\\&c^2=a^2+b^2\\&\\&c^2=9+18=27\\&\\&c= \sqrt {27}= 3 \sqrt 3\\&Focos:\\&(-3,3+3 \sqrt 3)\\&(-3, 3- 3 \sqrt 3)\\&\\&Vértex===> x=-3\\&\\&\frac{(y-3)^2}9- \frac{(x+3)^2} {18}=1\\&\frac{(y-3)^2}9=1\\&\\&(y-3)^2=9\\&\\&y-3= \pm 3\\&\\&y_1=6 ===> V_1=(-3,6)\\&\\&y_2=3-3=0 ===> V_2=(-3,0)\\&\end{align}$$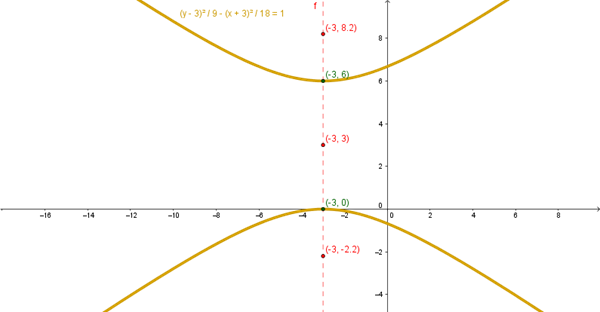

Saludos

;)

;)