Un rectángulo y en la parte superior un triángulo el perímetro es igual 3 y me piden determinar lado triángulo para averiguar el

Sergio, veamos lo que tenemos y a lo que podemos llegar, primero voy a hacer una imagen para entender lo que tengo y lo que necesitamos:

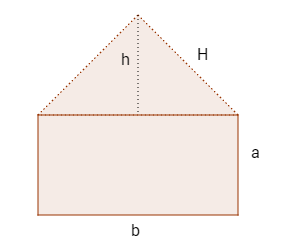
$$\begin{align}&\text{Sabemos que el perímetro es 3, o sea:}\\&3 = b + 2a + 2H......(1)\\&\text{Además la fórmula del área es}\\&A = ab + bh/2 \text{ (es lo que queremos maximizar)}\\&\text{Finalmente, sabemos que para H, podemos usar la fórmula}\\&H^2=h^2+(b/2)^2....(2)\\&Reemplazamos\ (2)\ en\ (1)\\&3 = b + 2a + 2(\sqrt{h^2+(b/2)^2}) \to\\&a=\frac{3-b-2(\sqrt{h^2+(b/2)^2})}{2}...(3)\\&\text{Reescribamos la fórmula para el área}\\&A(a,b,h) = b(a + h/2)\\&A = b\bigg(\frac{3-b-2(\sqrt{h^2+(b/2)^2})}{2}+\frac{h}{2} \bigg)\\&A(b,h) = b\bigg(\frac{3+h-b-2(\sqrt{h^2+(b/2)^2})}{2} \bigg)\end{align}$$

y queda para maximizar una expresión de 2 variables, por lo que revisa el enunciado para ver si no omitiste algo

Salu2