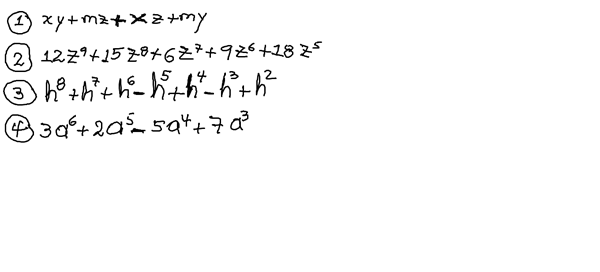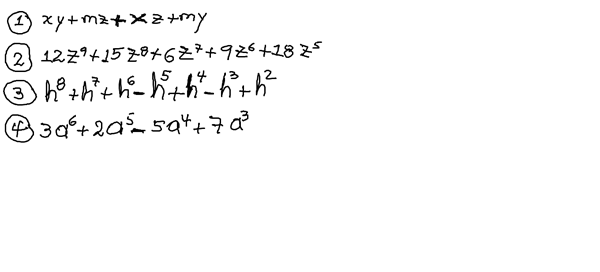Es un Taller de matemáticas

$$\begin{align}&1)\quad  xy +mz +xz+my= x(y+z)+m(z+y)=(y+z)(x+m)\\&\\&\\&2)\text{  Tomamos el máximo común divisor de los números y las letras}\\&\text{El máximo común divisor de los números es 3, todos son múltiplos de 3,}\\&\text{pero de 6, 9 o mayores siempre hay alguna que no lo es}\\&\text{Y el máximo común divisor en la misma letra con diversos exponentes}\\&\text{es la letra elevada al menor de los exponentes }z^5\\&\\&12z^9+15z^8+6z^7+9z^6+18z^5=3z^5(4z^4+5z^3+2z^2+3z+6)\\&\\&3)\quad \text{Todos los coeficientes son 1 o -1 su MCD es 1}\\&h^8+h^7+h^6-h^5+h^4-h^3+h^2= h^2(h^6+h^5+h^4-h^3+h^2-h+1)\\&\\&4)\quad\text{Los coeficientes son primos entre si, el MCD es 1}\\&3a^6+2a^5-5a^4+7a^3 = a^3(3a^3+2a^2-5a+7)\end{align}$$

·

·

¡Hola Juan David!

Veo que la respuesta fue a parar arriba, es un fallo de la página engorroso de corregir, pero ahí la tienes.

Sa lu dos.

:

:

1)  x.y + m.z + x.z +m.y

      x.y +m.y+ m.z + x.z 

      y,(x+m) + z (m+x)

       (x + m),(y + z)

Disculpa en este momento debo de salir pero lo demás es factorizar

2) Factoriza Z a la quinta

3) Factoriza h al cuadrado

4) Factoriza a al cubo