Ejercicio con funciones, asíntotas, intervalos de crecimiento y concavidad y convexidad

;)
Hola Yolanda!

Domf(x)=R-{-3}

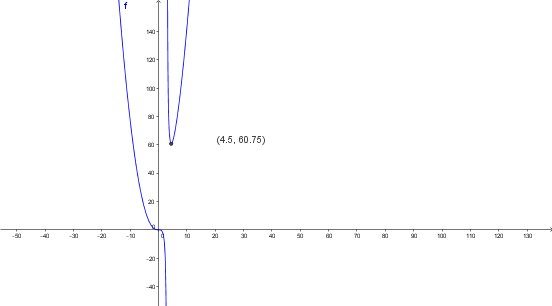
$$\begin{align}&\lim_{x \to 3}\frac{x^3}{x-3}= \frac {27} 0= \infty\\&\\&Asintota \ vertical:\ \ x=3\\&\\&\lim_{x \to \pm \infty}f(x)= + \infty ==> No \ hay\ asíntotas \ horizontales\\&\\&b)\\&y'=\frac{3x^2(x-3)-x^3}{(x-3)^2}= \frac{2x^3-9x^2}{(x-3)^2}=\frac{x^2(2x-9)}{(x-3)^2}\\&\\&y'=0\\&\frac{x^2(2x-9)}{(x-3)^2}=0==>x^2(2x-9)=0\\&\\&x_1=0\\&x_2= \frac 9 2\\&Ingtervalos \ de \ crecimiento:\\&(-\infty,0)=>f'(-10)<0 ==> \ decreciente\\&\\&(0,3)=> f'(1)<0==> \ decreciente\\&\\&(3, \frac 9 2) => f'(4)<0 ==> decreciente\\&\\&( \frac 9 2, + \infty)=> f'(10)>0 ==>creciente\\&\\&Mínimo \ relativoº en ( \frac 9 2,f( \frac 9 2))=(\frac  9 2, \frac {243} 4)\\& Punto \ inflexión \ con \ tangente \ horizontal \ en (0,0)\\&\\&c)\\&Concavidad \\&\\&y''=\frac{(6x^2-18x)(x-3)^2-2(x-3)(2x^3-9x^2)}{(x-3)^4}=\\&\\&\frac{ (6x^2-18x)(x-3)-2(2x^3-9x^2)}{(x-3)^3}=\frac{2x^3-18x^2+54x}{(x-3)^3}\\&y''=0\\&2x^3-18x^2+54x=0\\&2x(x^2-9x+27)=0\\&\\&x=0\\&\\&Intervalos \ concavidad:\\&(- \infty,0)=>y''(-10)>0===>Cóncava (hacia \ arriba) \cup\\&(0,3)=>y''(1)<0==>Convexa(\cap)\\&(3,+\infty)=>y''(10)>0==> \cup\\&punt Inflexió(0,0)\\&\\&\end{align}$$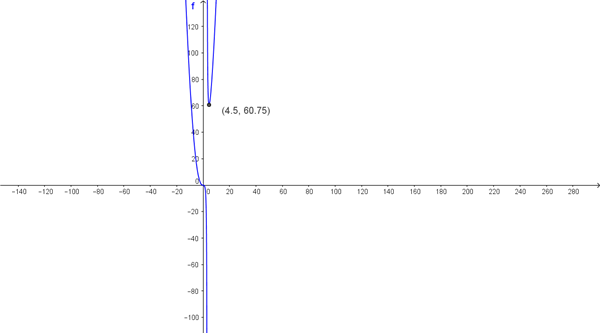

Saludos

;)

;)