Como se resuelve la suma de Riemann para f(x)=x^2-1 en intervalo [2,4].

;)
Hola Feli Feli!

Eso que ha hecho el otro experto no es una suma de Rieman

Tendrías que indicar por lo menos la Partición, y estaría bien si la quieres por laizquierda o por la derecha

;

La suma de Rieman la solicitan por la derecha.

;)
¿Y la partición?

¿La qué queramos?

  No  especifica detalles.

;)
Bueno, supongo que quieres el valor exacto, es decir cuando el numero de rectángulos n tiendea infinito:

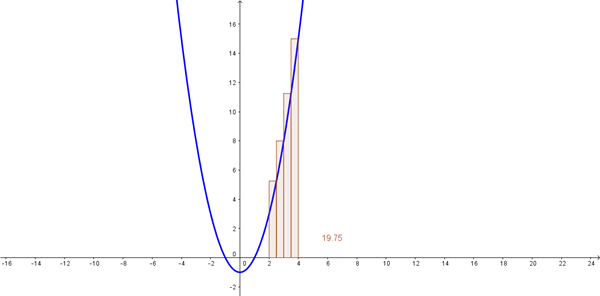
Esa sería una suma para una partición n=4

Hagamos la para una partición n:

Ancho de cada partición:

$$\begin{align}&\Delta= \frac{b-a} n=\frac {4-2} 2=2\\&\\&Abscisa \ del \ extremo \ derecho \ de \ cada \ subintervalo:\\&\\&x_i=a+\Delta x\\&\\&i\ indicaría \ el \ número \ del \ intervalo \ de\ izquierda \ a \ derecha\\&\\&x_i=2+i \frac 2 n\\&\\&La n-ésima   \ Suma \ de \ Riemann:\\&\\& \sum  _{i=1}^n f(x_i)· \Delta x= \sum  _{i=1}^n f(2+i \frac 2 n)· \frac 2 n=\\&\\&\sum  _{i=1}^n  \Bigg[ \Bigg(2+2 \frac i n \Bigg)^2-1 \Bigg] \frac 2 n=\\&\\&\sum  _{i=1}^n  \Bigg[ \Bigg(4+ 8 \frac i n+4 \frac{i^2}{n^2} \Bigg)-1 \Bigg] \frac 2 n=\\&\\&las \ constantes \ salen \ fuera \ del \ sumatorio:\\&\\&\frac 2 n \sum  _{i=1}^n  \Bigg(3+8  \frac i n +4 \frac{i^2}{n^2} \Bigg)\end{align}$$

El sumatorio de los números naturales está al alcance de todos mediante la fórmula de la suma de una sucesión artimética.

$$\begin{align}&S= \frac{n(n+1)} 2\\&\end{align}$$

Para la suma de los cuadrados no es tan sencillo, aunque es probable que hayas visto la fórmula en el tema de demostraciones por inducción.

Sin más te doy la fórmula que la puedes encontrar en Internet

$$\begin{align}&S_2= \frac {n(n+1)(2n+1)} 6\end{align}$$

$$\begin{align}&==\\&\\&\frac 2 n \Bigg( \sum  _{i=1}^n3 +\sum  _{i=1}^n 8 \frac i n+\sum  _{i=1}^n 4 \frac{i^2}{n^2} \Bigg)=\\&\\&\frac 2 n \Bigg( 3n+ \frac 8 n \frac {n(n+1)} 2+ \frac 4 {n^2}· \frac{n(n+1)(2n+1)} 6\Bigg)=\\&\\&6+8 \frac{(n+1)} n+ \frac 8 6 \frac{(n+1)(2n+1)} {n^2}=\\&\\&6+8+\frac 8 n+ \frac 4 3 \frac{2n^2+3n+1}{n^2}=\\&\\&14+\frac 8 n+ \frac 4 3 \Big( 2+ \frac 3 n+ \frac 1 {n^2} \Big)\\&\\&La  \ Suma \ Riemann \ es\ cuando \ \lim_{n\to \infty}\\&Solo \ quedan \ los \ terminos \ \sin \ n \ en \ denominador\\&\\&\lim_{n\to \infty}S_n=14+ \frac 8 3= \frac{50} 3=16, \overline 6\end{align}$$

;)
Copie mal(error tipográfico)

El ancho de la partición es

$$\begin{align}&\Delta x= \frac{b-a} n= \frac 2 n\end{align}$$

;)

Es muy sencillo. Primero calculas la primitiva y después la evalúas en el intervalo dado.

$$\begin{align}&\int_a^b f(x)=\int _2^4 (x^2-1) dx=\int_2^4x^2dx-\int_2^41dx\end{align}$$

Hay que separar las integrales puesto que es una resta y operamos con normalidad

$$\begin{align}&\int_2^4x^2dx-\int_2^41dx=[\frac{x^3}{3}]_2^4-[x]_2^4=[4^3/3-2^3/3]-[4-2]=[64-8]/3-2=56/3-6/3=50/3=16.666\end{align}$$

Si tienes alguna pregunta no dudes en preguntar.

De acuerdo a lo que he avanzado me queda diferente, solo que ya no pude avanzar en la sumatoria.

En este punto ya no pude continuar, pero tiene razón es una resta y tal vez yo lo estoy haciendo mal. Ud. ¿qué opina?

   Me atore en la sumatoria.