Se considera la curva definida por la función f(x)= 1-(3x/(x^2-4))

;)
Hola Miriam!

1) Es una función racional, el dominio son todos los Reales menos las raíces del denominador

$$\begin{align}&x^2-4=0\\&x= \pm2\\&\\&Domf(x)=\mathbb R- \{\pm2 \}\\&\\&Corte \ eje \OX ==> y=0=\\&\\&1- \frac {3x}{x^2-4}=0\\&\\&1=\frac {3x}{x^2-4}\\&\\&x^2-4=3x\\&x^2-3x-4=0\\&x_1=-1\\&x_2=4\\&\\&Corte \ Eje\ OY==> x=0==> f(0)=1-0=1\\&(0,1)\\&\\&Simetría:\\&f(-x)=1+ \frac{3x}{x^2-4} \neq f(x) ==> NO \ Par\\&\\&-f(x)=-1+ \frac {3x}{x^2-4} \neq f(-x) ==> No \ Impar\\&\\&2.-)\\&Asíntotas \ Horizontales\\&\lim_{x \to + \infty}1- \frac {3x}{x^2-4}=1-0=1\\&\\&\lim_{x \to - \infty}1- \frac {3x}{x^2-4}=1-0=1\\&Asint. Horiz.\\&y=1\\&\\&Asíntotas \Verticales\\& \lim_{x \to  \pm 2}1- \frac {3x}{x^2-4}=1-\frac 6 0=1 \mp \infty=\mp \infty\\&\\&Asíntotas\Verticales\\&x=2\\&x=-2\\&\\&\lim_{x \to -2^-}(1- \frac {3x}{x^2-4})=1+\frac 6 {+0}= +\infty\\&tambien \ puedes \ calcular\ f(-2,1) >0  (para \ visualizar \ el \ signo \ de \ ese \ infinito)\\&\\&\lim_{x \to -2^+}(1- \frac {3x}{x^2-4})=1+\frac 6 {-0}= -\infty\\&tambien \ puedes \ calcular\ f(-1,9) <0  (para \ visualizar \ el \ signo \ de \ ese \ infinito)\\&\\&\lim_{x \to 2^-}(1- \frac {3x}{x^2-4})=1-\frac 6 {-0}= +\infty\\&tambien \ puedes \ calcular\ f(1,9) >0  (para \ visualizar \ el \ signo \ de \ ese \ infinito)\\&\\&\lim_{x \to 2^+}(1- \frac {3x}{x^2-4})=1-\frac 6 {+0}= -\infty\\&tambien \ puedes \ calcular\ f(2,1) <0  (para \ visualizar \ el \ signo \ de \ ese \ infinito)\\&\\&3) Discontinuidades \ Asíntóticas\ en \\&x=2\\&x=-2\\&\\&4)\\&f'(x)=\frac {3x^2+12}{(x^2-4)^2}\\&extremos relativos==> f'(x)=0\\&\\&\frac {3x^2+12}{(x^2-4)^2}=0\\&\\&3x^2+12=0\\&\\&x^2=-4 ==>\not \exists \extremos\\&\\&intervalos \Crecimiento:\\&(-\infty,-2)==> f'(-10)>0 ==> creciente\\&\\&(-2,2)==> f'(0)>0 ==> creciente\\&\\&(2,+\infty))==> f'(10)>0==> creciente\\&\\&\end{align}$$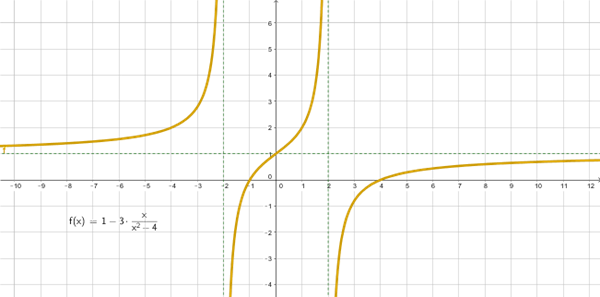

Saludos

;)

;)

Solo una duda, cuando pide estudiar la discontinuidad ¿,se trata de una discontinuidad de tipo inevitable?