Ahora tengo dudas en calculo, sumas de Riemann

;)
Hola recce!

En la suma de riemann izquierda tomamos como altura de los rectángulos las imágenes del punto extremo de los intervalos:

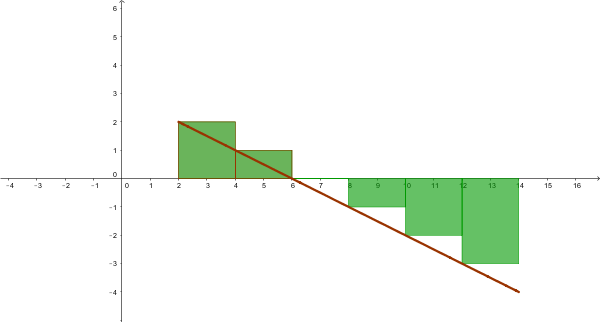
Además como hay un trozo de la función que es negativa, en esos puntos la altura será el valor absoluto de las imagenes. Recuerda que las sumas de Riemann son una aproximación a las áreas y un área no es negativa:

$$\begin{align}&\int_a^bf(x)dx \simeq  \sum_{i=0}^{n-1} f(x_{i-1}) \Delta x= \Delta x  \sum_{i=0}^{n-1} f(x_{i-1})\\&\\&\Delta x= \frac{b-a} n= \frac{14-2} 2=2\\&\\&intervalos:\\&[2,4] ==> f(2)=3- \frac 1 2 2=3-1=2\\&\\&[4,6] ==> f(4)=3- \frac 1 24=3-2=1\\&\\&[6,8] ==> f(6)=3 - \frac 1 2 6=0\\&\\&[8,10] ==> f(8)=3- \frac 1 28=-1\\&\\&[10,12]==> f(10)=-2\\&\\&[12,14] ==> f(12)=-3\\&\\&\int_2^{14}f(x)dx \simeq  \sum_{i=0}^{5} f(x_{i-1}) \Delta x= \Delta x  \sum_{i=0}^{5} f(x_{i-1})=\\&\\&\Delta x \Big[f(x_0)+f(x_1)+f(x_2)+f(x_3)+f(x_4)+f(x_5) \Big]=\\&\\&2 \Big[ 2+1+0+1+2+3 \Big]=2·9=18\\&\\&\end{align}$$

También se podría interpretar la suma de Riemann como aplicación literal de la fórmula , sin que esté aplicada para el cálculo aproximado del área, en cuyo caso:

$$\begin{align}&\Delta x \Big[f(x_0)+f(x_1)+f(x_2)+f(x_3)+f(x_4)+f(x_5) \Big]=\\&\\&2 \Big[ 2+1+0-1-2-3 \Big]=2·(-3)=-6\end{align}$$

Depende como te lo hayan explicado en clase

Saludos

;)

;)