Ecuación de la parábola con foco en (3,-1) y directriz la recta x=-1/2
Las respuestas están en la forma general de la ecuación
$$\begin{align}&(A) \ \ \ \ y^2-6y+2x+11=0\\&\\&(B) \ \ \ \ y^2+2y-14x+43=0\\&\\&(C) \ \ \ \ 2x^2-12x+y+19=0\\&\\&(D)\ \ \ \ 2x^2+12x-7y+25=0\\&\end{align}$$
1 Respuesta
;)
Hola Gabriel!
Para escribir la ecuación necesitamos saber tres cosas:
1) Vértice
b) p
c) Vertical/horizontal
La directriz es una recta vertical luego el eje focal es horizontal. Tenemos una parábola tipo
(y-k)^2=4p(x-h)
el eje focal se encuentra en la recta y=-1.
Recuerda también que elFoco se encuentra dentro de la parábola, luego abre hacia la derecha ==> p>0
El Vértice está en la mitad del Foco y la directriz:
$$\begin{align}&x=\frac{3+(-\frac 1 2)} 2= \frac 5 4\\&\\&V=(\frac 54 ,-1)=(h,k)\\&\\&El \ parámetro \ p \ es \ la\ distancia \ del \ Vértice \ al \ Foco:\\&\\&p=3- \frac 5 4= \frac 7 4\\&\\&(y+1)^2=4 \frac 7 4(x- \frac 5 4)\\&\\&(y+1)^2=7(x- \frac 5 4)\\&\\&y^2+2y+1=7x- \frac {35} 4\\&sacando \ los \ denominadores(multiplicándola \ por \ 4)\\&\\&4y^2+8y+4=28x-35\\&\\&4y^2+8y-28x+39=0\\&\\&\end{align}$$Que no se parece a ninguna de esos.
La voy a construir con GeoGebra:
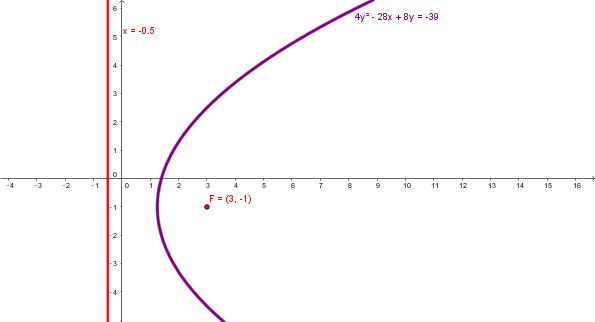
Mi resultado es correcto.
La parábola con directriz x=-1/2 y Foco(3,-1) es la que yo he obtenido.
Luego o se han equivocado al dar los datos, o al poner las soluciones
Saludos
;)
;)
Muchas gracias Lucas m cuando hallas vértice, halla valor solo para h o x, ¿por qué?
Por que -1 a la coordenada k ?Esa parte no la entiendo :(
;)
Observa que tanto el foco como el vértice se encuentran en la misma recta(eje focal) que es perpendicular a la directriz. Luego en el momento que se que la parábola es horizontal la y del foco y del vértice ya sé que son iguales==> y=-1
