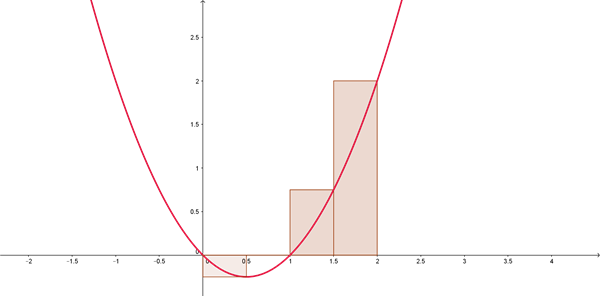
Ejercicio de evaluar la siguiente suma de riemann
Con 4 sub-intervalos, tomando los puntos extremos de la derecha como
Puntos muestra
$$\begin{align}&f(x)= x^2-x\end{align}$$$$\begin{align}& 0 ≤x≤2\\&\end{align}$$
1 respuesta
Respuesta de Lucas m
1
;)
Hola recce!
La suma de Riemann derecha es:
$$\begin{align}&\int_0^2 f(x)dx \simeq \sum_{i=1}^4 f(x_i) \Delta x\\&\\&\Delta x=\frac{b-a}n= \frac{2-0} 4= \frac 1 2\\&\\&Intervalos\\&[0,1/2] ==> f( \frac 1 2)= \frac 1 4 - \frac 1 2= -\frac 1 4\\&[ \frac 1 2,1]==> f(1)=0\\&[1, \frac 3 2]==> f( \frac 3 2)= \frac 9 4 - \frac 3 2= \frac 3 4\\&\\&[ \frac 3 2, 2]==> f(2)=4-2=2\\&\\&\int_0^2 f(x)dx \simeq \sum_{i=1}^4 f(x_i) \Delta x=\\&\\&\frac 1 2 \sum_{i=1}^4 f(x_i) = \frac 1 2 \Big[- \frac 1 4+0+ \frac 3 4+2 \Big]= \frac 5 4\\&\end{align}$$Eso sería la Suma de Riemann en sentido estricto; ahora bien si lo que quieres es el área aproximada por Riemann, evidentemente el -1/4 lo tendrías que poner positivo.
Depende de como te lo haya explicado el profesor
Saludos
;)
;)
