Un depósito contiene 500 lt de líquido en el que se disuelven 20 gr de sal: Una salmuera que contiene 5 gr/lt

;
Hola Juan!

Primero has de entender la ecuación diferencial que regula este proceso:

Lee atentamente lo siguiente hasta llegar a la ecuación diferencial

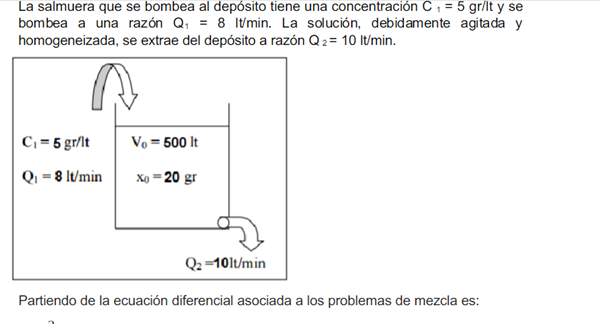
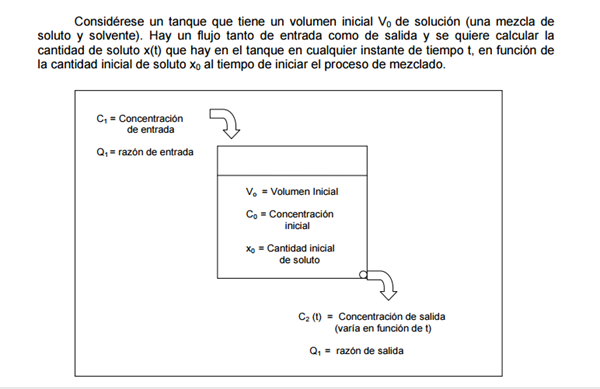
Esta es la ecuación diferencial que tenemos que resolver con los datos de nuestro problema:

$$\begin{align}&\frac{dx}{dt}+ \frac {Q_2}{V_0+(Q_1-Q_2)t}x(t)=Q_1C_1\\&\\&\frac{dx}{dt}+ \frac {10}{500+(8-10)t}x(t)=8·5\\&\\&simplificando:\\&\\&\frac{dx}{dt}+ \frac {5}{250-t}x(t)=40\\&\\&despejando:\\&\frac{dx}{dt}=40-\frac {5}{250-t}x(t)\\&\\&dx+ \frac 5 {250-t}x dt=40dt\ \ (*)\\&Ecuación \ Diferencial\ Lineal\ de\ la \ forma\ :x'+F(t)x=G(t)\\&\\&donde\\&\\&F(t)=\frac 5 {250-t}x \ \ i\\&G(t)=40\\&Se\ integra\ \ con\ Factor\ Integrante \mu\\& \int F(t)dt=\int \frac 5{250-t}dt=-5ln|250-t|\\&\\&\mu=e^{-5ln|250-t|}=(250-t)^{-5}\\&\\&Multiplicando\ ED(*)\ por \mu\\&\\&(250-t)^{-5}dx+(250-t)^{-5} \frac 5 {250-t}x dt=40(250-t)^{-5}dt\\&\\&(250-t)^{-5}dx+5(250-t)^{-6} x dt=40(250-t)^{-5}dt\ \ (**)\\&Que \es \diferencial\exacta \ ya \que\\&\\&(250-t)^{-5}dx+5(250-t)^{-6} x dt=d\Big[(250-t)^{-5}x \Big]\\&\\&sustituyendo\ en  \ (**)\\&d\Big[(250-t)^{-5}x \Big]=40(250-t)^{-5}dt\\&\\&Integrando:\\&\int d\Big[(250-t)^{-5}x \Big]=\int 40(250-t)^{-5}dt\\&inmediatas:\\&\\&(250-t)^{-5}x=\frac{40(250-t)^{-4}}{-4(-1)}\\&\\&(250-t)^{-5}x={10(250-t)^{-4}}+K\ \ (***)\\&K:constnte\integración.\ De\ la \ condición \ inicial \ t=0\==>x=20gr\\&\\&x(0)=20\\&sustituyendo\\&250^{-5}·20=10·250^{-4}+K\\&\\&K=\frac{20}{250^5}- \frac{10}{250^4}=\frac{20-2500}{250^5}=\frac{-2480}{250^5}=-(250^{-5})2480\\&\\&Este \ valor \ se \ sustituye\ en \ (***)\\&\\&(250-t)^{-5}x={10(250-t)^{-4}}-2480(250)^{-5}\\&\\&Multiplicandola\ por \ (250-t)^{5}:\\&\\&x= 10(250-t)-2480\Big(\frac{250-t}{250} \Big)^5\\&\\&Que\ es \ la \ ley \ de \ variación \ de \ gr \ de \ sal\ en\ el \ depósito\ en \ el\ instante\ t\\&\\&Finalmente\ la \ concentración:\\&\\&C(t)= \frac{x(t)}{V(t)}\\&\\&V(t)=V_0+(Q_1-Q_2)t=500-2t=2(250-t)\\&\\&Sustituyendo:\\&\\&C(t)=\frac{10(250-t)-2480\Big(\frac{250-t}{250} \Big)^5}{2(250-t)}=5-1240 \frac{(250-t)^4}{250^5}\\&\end{align}$$

Repasa las cuentas.

Menudo problemilla!

Saludos y recuerda votar

;)

;)