Calcula la integral mediante sustitución trigonométrica

;)
Hola Ume Lee!

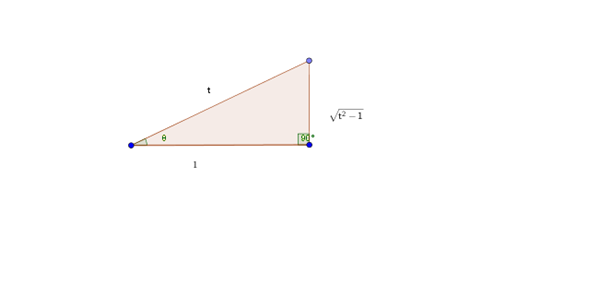
$$\begin{align}&sec \theta=t\\&sec \theta tan \theta d \theta=t\\&\sqrt {t^2-1}= \sqrt {sec^2 \theta -1}=identidad\ trigonometrica=\sqrt {tan^2 \theta}= tan \theta\\&\\&\int \frac   1 {t^3 \sqrt {t^2-1}}dt= \int \frac 1 {sec^3 \theta· tan \theta}sec \theta tan \theta d \theta=simplificando\\&\\&\int \frac 1 {sec^2 \theta} d \theta= \int \cos ^2 \theta d \theta= identidad \ trigonometrica=\\&\\&\int \frac{1+cos2 \theta} 2 d \theta=\\&\\&\frac 1 2 \int [1+ \cos (2 \theta)]  d \theta= \\&\\&\frac 1 2 \Big[ \theta + \frac 1 2 \sin 2 \theta \Big]===\\&\\&angulodoble: \sin(2 \theta)=2 \sin \theta \cos \theta\\&\cos \theta= \frac 1 t ==> \sin \theta=\sqrt {1- \frac 1 {t^2}}=\sqrt { \frac {1-t^2}{t^2}}= \frac 1 t \sqrt {1- t^2}\\&\sin(2 \theta)=2 \sin \theta \cos \theta= 2 \frac 1 t \sqrt {1- t^2} \frac 1 t= \frac 2 {t^2} \sqrt {1-t^2}\\&\\&=== \frac 1 2 \Big[ arc \sin \theta+ \frac 1 2 \frac 2 {t^2} \sqrt {1-t^2} \Big ] +C=\\&\\&\frac 1 2 \Big[ arc \sin \theta+ \frac 1{t^2} \sqrt {1-t^2} \Big ] +C\\&\end{align}$$

Saludos

;)

;)

;)
En la segunda línea

$$\begin{align}&sec \theta tan \theta d \theta= dt\end{align}$$

me deje la d del diferencial dt

;)