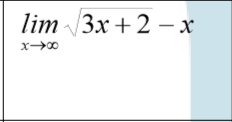Como resuelvo el siguiente ejercicio de limites al infinito?

En éstos casos, debemos multiplicar por su conjugado, es decir

$$\begin{align}&\lim_{x\rightarrow\infty}{(\sqrt{3x+2}-x)\left(\frac{\sqrt{3x+2}+x}{\sqrt{3x+2}+x}\right)}=\lim_{x\rightarrow\infty}{\left(\frac{3x+2-x^{2}}{\sqrt{3x+2}+x}\right)}=\frac{\infty}{\infty}\end{align}$$

ya hemos multiplicado por el conjugado y nos quedó esa igualdad...y calculando el límite nos queda esa indeterminación...la forma más fácil de atacar el problema es usando L`Hopital, es decir vamos a derivar el numerador y el denominador, y veremos si con eso podremos hallar el límite...OJO, éste proceso se lo puede aplicar siempre y cuando tengas indeterminaciones del tipo infinito entre infinito o cero entre cero, bien,

$$\begin{align}&\lim_{x\rightarrow\infty}{\frac{f(x)}{g(x)}}=\lim_{x\rightarrow\infty}{\frac{3x+2-x^{2}}{\sqrt{3x+2}+x}}=\lim_{x\rightarrow\infty}{\frac{3-2x}{\frac{3}{2\sqrt{3x+2}}+1}}=\lim_{x\rightarrow\infty}{\frac{f'(x)}{g'(x)}}=\lim_{x\rightarrow\infty}{\frac{3-2x}{\frac{3}{2\sqrt{3x+2}}+1}}={\frac{3-2(\infty)}{\frac{3}{2\sqrt{3(\infty)+2}}+1}}=\frac{-\infty}{0+1}=-\infty\end{align}$$

y ese es el límite de ña función...

Debes tener en cuenta que si infinito es un número extremadamente gigantesco entonces cualquier número entre infinito es cero... puedes intentar en la calculadora divide por ejemplo 577 entre 217361273176253712 y ese valor es muy cercano a cero... ésto es lo que sucede en el dneominador hay esa derivada de la raíz y se hace cero... y eso sería todo

;)
Vota primero

;)