Como resolver ejercicios de integrales impropias
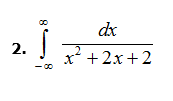
Resolver el siguiente ejercicio de integrales impropias aplicando la teoría
1 respuesta
Respuesta
1
